
如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE= AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.

(1)证明见解析;
(2)证明见解析;
(3)BO=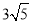 .
.
【解析】
试题分析:(1)根据等角的余角相等证明即可;
(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;
(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt△BDO中,利用勾股定理列式求解即可.
试题解析:(1)∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠ABP,
∵∠BOC=∠AOP,
∴∠AOP=∠ABP,
∴AP=AO;
(2)如图,过点O作OD⊥AB于D,
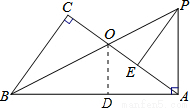
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
∵AE=OD,∠AOD=∠PAE,AP=AO,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO;
(3)设AE=OC=3k,
∵AE=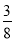 AC,∴AC=8k,
AC,∴AC=8k,
∴OE=AC﹣AE﹣OC=2k,
∴OA=OE+AE=5k.
由(1)可知,AP=AO=5k.
如图,过点O作OD⊥AB于点D,
∵∠CBO=∠ABP,∴OD=OC=3k.
在Rt△AOD中,AD=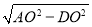 =
=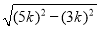 =4k.
=4k.
∴BD=AB﹣AD=10﹣4k.
∵OD∥AP,
∴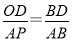 ,即
,即
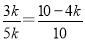 ,
,
∵AB=10,PE=AD,
∴PE=AD=4K,BD=AB﹣AD=10﹣4k,
由∠CBO=∠ABP,根据轴对称BC=BD=10﹣4k,
∵∠BOC=∠EOP,∠C=∠PEO=90°,
∴△BCO∽△PEO,
∴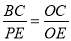 ,
,
即 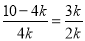 ,
,
解得k=1.
∴BD=10﹣4k=6,OD=3k=3,
在Rt△BDO中,由勾股定理得:
BO=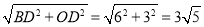 .
.
考点:1.相似三角形的判定与性质2.全等三角形的判定与性质3.角平分线的性质4.等腰三角形的判定与性质.


科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:解答题
某地要在规定的时间内安置一批居民,若每个月安置12户居民,则在规定时间内只能安置90%的居民户;若每个月安置16户居民,则可提前一个月完成安置任务,问要安置多少户居民?规定时间为多少个月?(列方程(组)求解)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:选择题
小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是( )
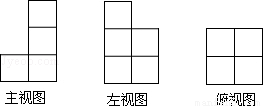
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:选择题
餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
A.5×1010千克 B.50×109千克 C.5×109千克 D.0.5×1011千克
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川眉山卷)数学(解析版) 题型:填空题
某种生物孢子的直径为0.00058m.把0.00058用科学记数法表示为______________.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:选择题
在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形AOB的面积是( )
(A)
 (B)
(B)
 (C)
(C)
 (D)
(D)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com