【题目】如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．

（1）用直尺画出该圆弧所在圆的圆心M的位置；

（2）若A点的坐标为（0，4），D点的坐标为（7，0），试验证点D是否在经过点A、B、C的抛物线上；

（3）在（2）的条件下，求证：直线CD是⊙M的切线．

参考答案：

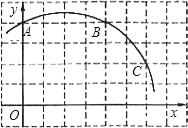
【答案】(1)画图参见解析；（2）不在；（3）证明参见解析.

【解析】

试题分析：（1）利用“两弦垂直平分线的交点为圆心”可确定圆心位置；（2）先根据A、B、C三点坐标，用待定系数法求出抛物线的解析式，然后将D点坐标代入抛物线的解析式中，即可判断出点D是否在抛物线的图象上；（3）由于C在⊙M上，如果CD与⊙M相切，那么C点必为切点；因此可连接MC，证MC是否与CD垂直即可．可根据C、M、D三点坐标，分别表示出△CMD三边的长，然后用勾股定理来判断∠MCD是否为直角．

试题解析：（1）如下图，连接AB,BC，作线段AB,BC的垂直平分线，两线的交点M即为所求；（2）由A（0，4），可得小正方形的边长为1，从而B（4，4）、C（6，2）,设经过点A、B、C的抛物线的解析式为y=ax2+bx+4

依题意，解得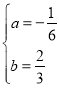,所以经过点A、B、C的抛物线的解析式为y=﹣x2+x+4,把点D（7，0）的横坐标x=7代入上述解析式，得y=-×49+×7+4=≠0,所以点D不在经过A、B、C的抛物线上；（3）如图，设过C点与x轴垂直的直线与x轴的交点为E，连接MC，作直线CD

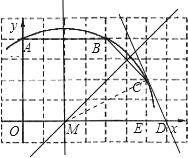
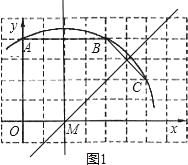
由图可知：CE=2，ME=4，ED=1，MD=5,在Rt△CEM中，∠CEM=90°,∴MC2=ME2+CE2=42+22=20,在Rt△CED中，∠CED=90°,∴CD2=ED2+CE2=12+22=5,∴MD2=MC2+CD2,∴∠MCD=90°,∵MC为半径,∴直线CD是⊙M的切线．

关闭