
 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4) =
= =5cm,
=5cm,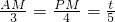 ,
, t,OM=OA-AM=3-
t,OM=OA-AM=3- t,
t, t,3-
t,3- t);
t); ×t×(3-
×t×(3- t)=-
t)=- t2+
t2+ t
t (t-
(t- )2+
)2+ ,
, 时,S有最大值,最大值为
时,S有最大值,最大值为 ;
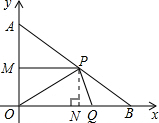
;
 ,
, t)2=
t)2= t(t-
t(t- t),
t), t,OQ=t,
t,OQ=t, t,
t, cm/s,
cm/s, t=
t= t•
t• ,
,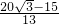 .
. OQ分别列式求解即可得到Q点运动速度和时间t.
OQ分别列式求解即可得到Q点运动速度和时间t.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
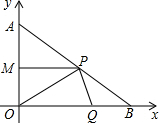 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=
如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•咸宁)如图,在Rt△AOB中,OA=OB=3
(2013•咸宁)如图,在Rt△AOB中,OA=OB=3| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设
(2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com