
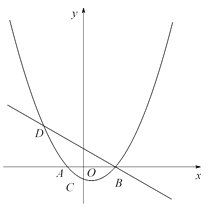
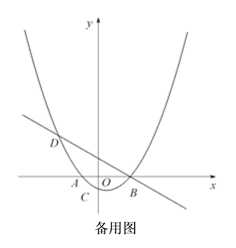
����Ŀ����ͼ����֪������![]() (aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��
(aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��![]() �������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
��1���������ߵĺ�������ʽ��
��2��PΪֱ��BD�·����������ϵ�һ�㣬����PD��PB, ����PBD��������ֵ��
��3����FΪ�߶�BD��һ��(�����˵�)������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡���1��![]() ����2��
����2��![]() ����3����F����Ϊ(��2��
����3����F����Ϊ(��2�� ![]() )ʱ����M�������˶���������ʱ���٣�
)ʱ����M�������˶���������ʱ���٣�
���������������: (1�����������A��B���꣬Ȼ����õ�D���꣬����������y=a��x+2����x-4����aΪ��������a��0������������߽���ʽ��
(2) ��P(m, ![]() ),���������ε������ʽ���ɵý⣻
),���������ε������ʽ���ɵý⣻
��3�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+![]() DF���������ߣ���AF+
DF���������ߣ���AF+![]() DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
���������(1)������![]() ��y��0�����x����2��x��4��
��y��0�����x����2��x��4��
��A(��2��0)��B(4��0)��
��ֱ��![]() ������B(4��0)��
������B(4��0)��
��![]() �����
�����![]() ��
��
��ֱ��BD����ʽΪ�� ![]() ��
��
��x����5ʱ��y��3![]() ��
��
��D(��5��3![]() )��
)��
�ߵ�D(��5�� ![]() )��������
)��������![]() �ϣ�
�ϣ�
��![]() ��
��
��![]() ��
��
�������ߵĺ�������ʽΪ�� ![]() ��
��
(2)��P(m, ![]() )
)
��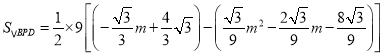
![]() ��
�� ![]()
���BPD��������ֵΪ![]() ����
����
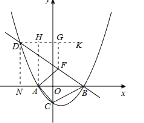
(3)��DK��AB��AH��DK��AH��ֱ��BD�ڵ�F��
����(2)�ã�DN��![]() ,BN��9�����á�DBA��30�������BDH��30����
,BN��9�����á�DBA��30�������BDH��30����
��FG��DF��sin30����![]() ��
��
�൱�ҽ���AH��DKʱ��AF+FH��С��
��M�������˶�����ʱΪ��t��![]() ��
��
��lBD�� ![]() ����Fx��Ax����2��F(��2��
����Fx��Ax����2��F(��2�� ![]() )
)
�൱F����Ϊ(��2�� ![]() )ʱ����ʱ���٣�
)ʱ����ʱ���٣�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��a��b���ڵ�һ���ޣ����P1��-a��-b���ڣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽ�������������������ٻص��ң�����ҵľ���y��ǧ�ף���ʱ��t�����ӣ��Ĺ�ϵ��ͼ��ʾ.�������ͼ��ش��������⣺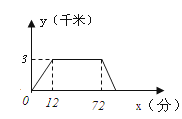
��1��С�����볬�еľ����Ƕ���ǧ�ף�
��2��С���ڳ�������ʱ��Ϊ����Сʱ��
��3��С��ȥ����ʱ���ٶ��Ƕ���ǧ��/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�ϵʽ����x2-3x=4����S=3.5t����y= ![]() ����y=5x-3����C=2��R����S=v0t+
����y=5x-3����C=2��R����S=v0t+ ![]() at2����2y+y2=0�����в��Ǻ�����ϵ���ǣ� ��
at2����2y+y2=0�����в��Ǻ�����ϵ���ǣ� ��
A.�٢�
B.�٢ڢۢ�
C.�ܢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����.����ͬѧ�����г���A����ͬһ��·��B��,��֪�ұȼ��ȳ���,����������صľ���S(km)������ʱ��t(h)֮��ĺ�����ϵ��ͼ1��ʾ,��������˵��:�����Ƕ�������20km;������;��ͣ����0.5h;�ۼ�.������ͬʱ����Ŀ�ĵ�;��������,���ٶ�С���ҵ��ٶ�.
����ͼ����Ϣ,����˵����ȷ���У� �� 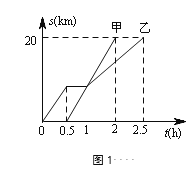
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㵺�Թž����й��������й������ѶԵ��㵺��չ��̬��Ѳ��.ij�죬Ϊ���ƻ��㵽��ָ������ijѲ��ͧ�賿1��00������������ʻһ��ʱ�������;���ֹ��ϵ�����һ��ʱ�䣬�����ų���ͧ�ӿ��ٶ�������ǰ�������ǡ���㵽��.��ͼ�Ǹ�ͧ��ʻ��·��![]() �����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
�����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
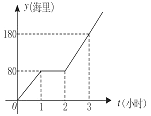
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����C����O��һ�㣬����C��ֱ�߽�AB���ӳ����ڵ�D��AE��DC������ΪE��F��AE����O�Ľ��㣬ACƽ����BAE��

��1����֤��DE����O�����ߣ�
��2����AE=6����D=30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С�ֻ������� ![]() ��һ����ͼ������ͼ��ش�
��һ����ͼ������ͼ��ش�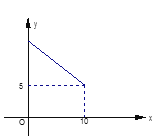
��1���Ա���x��ȡֵ��Χ.
��2����xȡʲôֵʱ��y����Сֵ.���ֵ���Ƕ��٣�
��3����ͼ�У���x����ʱ��y��ֵ�������仯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ����DE��AC��D����AB��E����DBC=15�㣬���A�Ķ����ǣ� �� 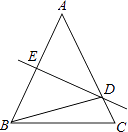
A.50��
B.20��
C.30��
D.25��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com