
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.

结论:(1)
(2)
选择结论: ,说明理由.
【答案】(1) ∠APC+∠PAB+∠PCD=360°(2)∠APC = ∠PAB+∠PCD;(2)
【解析】试题分析:(1)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,同旁内角互补,即可求得∠PAB+∠1=180°,∠2+∠PCD=180°,则可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;
(2)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD.
试题解析:(1)∠APC+∠PAB+∠PCD=360°.理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
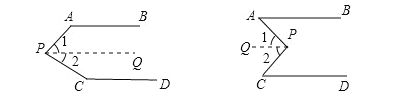
(2)∠APC=∠PAB+∠PCD.理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD.


科目:初中数学 来源: 题型:
【题目】一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数,中位数分别为( )
A. 3.5,3 B. 3,4 C. 3,3.5 D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店的老板均以60元的价格卖了两个计算器,其中一个赚了20﹪,另一个亏了20﹪,则该老板( )
A. 赚了5元 B. 亏了25元 C. 赚了25元 D. 亏了5元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a表示一个任意有理数,那么下面说法正确的是( )
A. ﹣a是负数 B. |a|一定是正数 C. |a|一定不是负数 D. |﹣a|一定是负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在边AB上,且∠DCE=45°
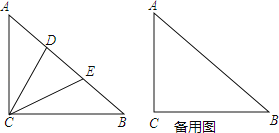
(1)以点C为旋转中心,将△ADC顺时针旋转90°,画出旋转后的图形;
(2)若AD=2,BE=3,求DE的长;
(3)若AD=1,AB=5,直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.

(1)CF= ;
(2)四边形AEFD是什么特殊四边形,你认为最准确的是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,你们知道“大白”吗?你们看过美国著名动画电影《超能陆战队》吗?该片在3月26日宣告内地票房累积达5.01亿,创造了迪士尼动画电影在中国内地的最高票房纪录,数据“5.01亿”用科学记数法表示为( )
A. 5.01×107 B. 5.01×108 C. 5.01×109 D. 50.1×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
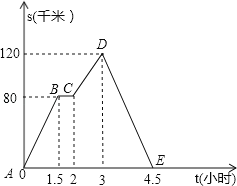
(1)汽车在DE段行驶了 小时;
(2)汽车在BC段停留了 小时;
(3)汽车出发1小时时,离出发地多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com