
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在边AB上,且∠DCE=45°
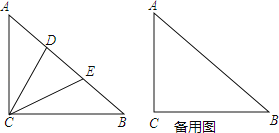
(1)以点C为旋转中心,将△ADC顺时针旋转90°,画出旋转后的图形;
(2)若AD=2,BE=3,求DE的长;
(3)若AD=1,AB=5,直接写出DE的长.
【答案】(1)见解析;(2)DE=![]() ;(3)DE的长为
;(3)DE的长为![]() .
.
【解析】
试题分析:(1)利用旋转的性质作图;
(2)连结EF,如图,先根据等腰直角三角形的性质得∠A=∠ABC=45°,再根据旋转的性质得CD=CF,BF=AD=2,∠DCF=90°,∠CBF=∠A=45°,则可根据“SAS”判断△DCE≌△FCE,得到DE=FE,然后在△BEF中利用勾股定理计算EF,从而得到DE的长;
(3)设ED=x,则BE=4﹣x,由(2)的证明得到EF=DE=x,BF=AD=1,然后在Rt△BEF中利用勾股定理得到12+(4﹣x)2=x2,再解方程即可.
解:(1)如图,△BCF为所作;
(2)连结EF,如图,
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵△ADC顺时针旋转90°得到△BCF,
∴CD=CF,BF=AD=2,∠DCF=90°,∠CBF=∠A=45°,
∵∠DCE=45°,
∴∠FCE=45°,
在△DCE和△FCE中
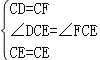 ,
,
∴△DCE≌△FCE,
∴DE=FE,
在△BEF中,∵∠EBC=45°,∠CBF=45°,
∴∠EBF=90°,
∴EF=![]() =
=![]() ,
,
∴DE=![]() ;
;
(3)∵AD=1,AB=5,
∵BD=4,
设ED=x,则BE=4﹣x,
由(2)得EF=DE=x,BF=AD=1,
在Rt△BEF中,12+(4﹣x)2=x2,解得x=![]() ,
,
即DE的长为![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】某校在开展“爱心捐助”的活动中,九年级一班六名同学捐款的数额分别为:8,10,10,4,8,10(单位:元),这组数据的众数是( )
A. 10 B. 9 C. 8 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
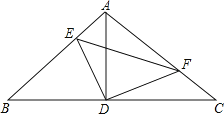
A.△ADF≌△BDE
B.S四边形AEDF=![]() S△ABC
S△ABC
C.BE+CF=![]() AD
AD
D.EF=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.

结论:(1)
(2)
选择结论: ,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,24,22,24,26,27,则这组数据的中位数与众数分别是( )
A. 23,24 B. 24,22 C. 24,24 D. 22,24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
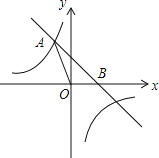
(1)求a、b的值;
(2)若点P在x轴上,且△AOP的面积是△AOB的面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com