
 实验室里,水平桌面上甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示,若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,求开始注入多少分钟的水量后,甲与乙的水位高度之差是0.5cm?
实验室里,水平桌面上甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示,若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,求开始注入多少分钟的水量后,甲与乙的水位高度之差是0.5cm? 分析 先找出一分钟丙的水位上升的高度,再分析当甲与乙的水位高度之差是0.5cm有几种情况,分情况列出方程,解出方程即可.
解答 解:∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,且注水1分钟,乙的水位上升$\frac{5}{6}$cm,
∴注水1分钟,丙的水位上升$\frac{5}{6}$×22=$\frac{10}{3}$cm.
设开始注入t分钟的水量后,甲与乙的水位高度之差是0.5cm,
甲与乙的水位高度之差是0.5cm有三种情况:
①当乙的水位低于甲的水位时,
有1-$\frac{5}{6}$t=0.5,
解得:t=$\frac{3}{5}$分钟;
②当甲的水位低于乙的水位时,甲的水位不变时,
∵$\frac{5}{6}$t-1=0.5,
解得:t=$\frac{9}{5}$,
又∵$\frac{10}{3}$×$\frac{9}{5}$=6>5.
∴此时丙容器已向乙容器溢水.
∵5÷$\frac{10}{3}$=$\frac{3}{2}$分钟,$\frac{5}{6}$×$\frac{3}{2}$=$\frac{5}{4}$,即经过$\frac{3}{2}$分钟丙容器的水到达管子底部,乙的水位上升$\frac{5}{4}$cm.
∴$\frac{5}{4}$+2×$\frac{5}{6}$(t-$\frac{3}{2}$)-1=0.5,
解得t=$\frac{33}{20}$;
③当甲的水位低于乙的水位时,乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为:$\frac{3}{2}$+(5-$\frac{5}{4}$)÷$\frac{5}{6}$÷2=$\frac{15}{4}$分钟,
∴5-1-2×$\frac{10}{3}$(t-$\frac{15}{4}$)=0.5,
解得:t=$\frac{171}{40}$.
综上所述,开始注水$\frac{3}{5}$、$\frac{33}{20}$、$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.
点评 本题考查一元一次方程的应用,解题的关键是:考虑当甲与乙的水位高度之差是0.5cm有几种情况,分情况列出方程.


科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,E为AB的中点,G、F分别为AD、BC上的点,若AG=2,BF=4,∠GEF=90°,则GF的长为( )
如图,正方形ABCD中,E为AB的中点,G、F分别为AD、BC上的点,若AG=2,BF=4,∠GEF=90°,则GF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
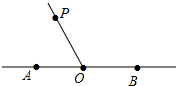 如图,下列语句中,描述错误的是( )
如图,下列语句中,描述错误的是( )| A. | 点O在直线AB上 | B. | 直线AB与射线OP相交于点O | ||
| C. | 点P在直线AB上 | D. | ∠AOP与∠BOP互为补角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2xy,$\frac{x-1}{3}$,a | B. | $\frac{x}{π}$,-2,$\frac{{a}^{2}b}{3}$ | C. | $\frac{1}{x}$,x2y,-m | D. | x+y,xyz,2a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com