
 求下列图形中∠CDE=________.
求下列图形中∠CDE=________. 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012年江苏省九年级中考模拟数学试卷2 题型:解答题
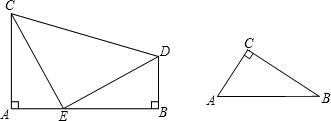
如图,已知:AC⊥AB,BD⊥AB,且AC=BE,AE=BD,求证:△CDE是等腰直角三角形;

证明:∵AC⊥AB,BD⊥AB ∴∠CAE=∠DBE=90°
∵AC= BE,AE=BD ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90° ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题:
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.
1.若BD=AC,AE=CD,在下图中画出符合题意的图形,求出∠APE的度数;
2.若AC=BD,CD=AE,则∠APE=__________°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com