
【题目】如图,已知某写字楼AB的正前方有一座信号塔DE,在高为60m的楼顶B处,测得塔尖E处的仰角为30°,从楼底A处向信号塔方向走30m到达C处,测得塔尖E处的仰角为68°,已知点D,C,A在同一水平线上,求信号塔DE的高度.(结果精确到0.1m.参考数据:sin68°≈0.9,cos68°≈0.4,tan 68°≈2.5,![]() ≈1.7).
≈1.7).
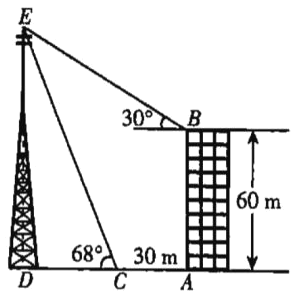
【答案】信号塔DE的高度约为101.5m.
【解析】
过点B作BG⊥DE于点G,设CD=xm,在△CDE中,得到DE=CD·tan 68°![]() (m),进而得到EG=DE-GD=(2.5x-60)m;在△EGB中,得到BG=
(m),进而得到EG=DE-GD=(2.5x-60)m;在△EGB中,得到BG=![]() EG=1.7(2.5x-60)m,因为BG=AD,所以1.7(2.5x-60)=x+30,求解即可.
EG=1.7(2.5x-60)m,因为BG=AD,所以1.7(2.5x-60)=x+30,求解即可.
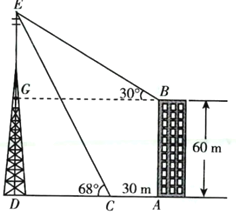
过点B作BG⊥DE于点G.
设CD=xm,
在△CDE中,∠EDC=90°,∠ECD=68°,
则![]() =tan 68°,
=tan 68°,
∴DE=CD·tan 68°![]() (m).
(m).
∵GD=AB=60m,
∴EG=DE-GD=(2.5x-60)m
在△EGB中,∠EGB=90°,∠EBG=30°
则![]() =tan 30°,
=tan 30°,
∴BG=![]() EG=1.7(2.5x-60)m.
EG=1.7(2.5x-60)m.
∴BG=AD,
∴1.7(2.5x-60)=x+30,
解得x=![]()
则DE=2.5×![]() =101.5(m).
=101.5(m).
答:信号塔DE的高度约为101.5m.


科目:初中数学 来源: 题型:
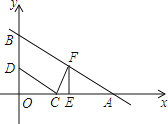
【题目】如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
(1)求这个一次函数的解析式;
(2)过点F作FE⊥x轴,垂足为点E,当△OCD与△EFC全等时,求出满足条件的点F的坐标;
(3)点D在运动过程中,是否存在使△ACF是等腰三角形?若存在请求出点F的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解禁毒知识宣传的效果,针对全校学生进行了一次测试,并随机抽取 了部分学生的测试成绩(满分100分,最低分为60分,80分及以上为优秀),统计后绘制成如下不完整的

请根据以上信息,解答下列问题:
(1)表中![]() __________,
__________,![]() _________;
_________;
(2)请补全频数分布直方图;
(3)若该校有学生2100人,试估计分数达到优秀的有多少人;
(4)学校准备从得分最高的5名学生(3男2女)中,随机挑选2名学生去参加市里举办的禁毒知识竞赛.小明说:“因为男生人数是女生人数的![]() 倍,所以选中的2名学生都是男生的概率是选中的2名学生都是女生的概率的
倍,所以选中的2名学生都是男生的概率是选中的2名学生都是女生的概率的![]() 倍.”他的说法正确吗?请判断并说明理由.
倍.”他的说法正确吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
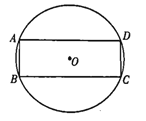
【题目】如图,⊙O为短形ABCD的外接圆,其半径为3.
(1)用尺规作图作出∠ABC的平分线,并标出它与劣弧AD的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦AD的距离为2,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
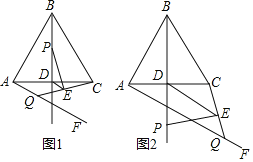
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,函数y=![]() (x>0)的图象G经过点A(4,1),与直线y=
(x>0)的图象G经过点A(4,1),与直线y=![]() x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
x+b的图象交于点B,与y轴交于点C.其中横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域(不含边界)为W.若W内恰有4个整点,结合函数图象,b的取值范围是( )
A.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]() B.﹣
B.﹣![]() ≤b<1或
≤b<1或![]() <b≤
<b≤![]()
C.﹣![]() ≤b<﹣1或﹣
≤b<﹣1或﹣![]() <b≤
<b≤![]() D.﹣
D.﹣![]() ≤b<﹣1或
≤b<﹣1或![]() <b≤
<b≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法.统计整理并制作了如下的统计图:
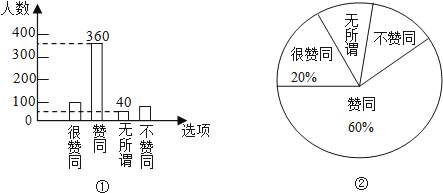
(1)这次调查的家长总数为__________,家长表示“不赞同”的人数为________________;
(2)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是____________;
(3)求图②中表示家长“无所谓”的扇形圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com