
分析 由勾股定理首先求得AB的长度,然后根据锐角三角函数的定义计算即可.
解答 解:由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{{5}^{2}+1{2}^{2}}$=13.
∴sinA=$\frac{BC}{AB}=\frac{12}{13}$,cosA=$\frac{AC}{AB}=\frac{5}{13}$,tanA=$\frac{BC}{AC}$=$\frac{12}{5}$,sinB=$\frac{AC}{AB}=\frac{5}{13}$,cosB=$\frac{BC}{AB}=\frac{12}{13}$,tanB=$\frac{AC}{CB}=\frac{5}{12}$.
点评 本题主要考查的是锐角三角函数的定义和勾股定理的应用,掌握锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
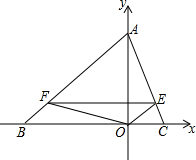 如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.
如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
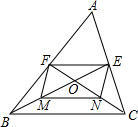 如图,BE,CF是△ABC的两条中线,它们相交于点O,M,N分别是OB,OC的中点,你能确定四边形FMNE是什么特殊四边形吗?请说明你的理由.
如图,BE,CF是△ABC的两条中线,它们相交于点O,M,N分别是OB,OC的中点,你能确定四边形FMNE是什么特殊四边形吗?请说明你的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com