
分析 由不等式ax2+bx+c>0的解集为x<2或x>3,可得2,3为方程ax2+bx+c=0的两根,利用根与系数的关系得到系数的比,变形后得到b=-5a,c=6a.由此求出方程bx2+ax+c的两根,则不等式bx2+ax+c>0的解集可求.
解答 解:∵不等式ax2+bx+c>0的解集为x<2或x>3,
∴2,3为方程ax2+bx+c=0的两个实数根,且a>0.
∴$\left\{\begin{array}{l}{-\frac{b}{a}=2+3}\\{\frac{c}{a}=2×3}\end{array}\right.$,
则b=-5a,c=6a.
代入不等式bx2+ax+c>0可得-5ax2+ax+6a>0,
∵a>0.
∴-5x2+x+6>0,即-(x+1)(5x-6)>0,
解得-1<x<$\frac{6}{5}$,
即不等式bx2+ax+c>0的解集是-1<x<$\frac{6}{5}$.
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,考查了推理能力和计算能力,属于基础题.


科目:初中数学 来源: 题型:解答题
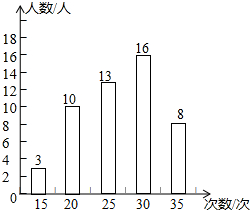 陕西省教育厅公布《陕西初中毕业生升学体育考试工作方案》,2015年中考体育测试项目增加三大球和单项运动技能,为了了解本校女生的体能情况,随机抽查了其中50名女生测试1分钟仰卧起坐的次数,并绘制成如图所示的统计图.
陕西省教育厅公布《陕西初中毕业生升学体育考试工作方案》,2015年中考体育测试项目增加三大球和单项运动技能,为了了解本校女生的体能情况,随机抽查了其中50名女生测试1分钟仰卧起坐的次数,并绘制成如图所示的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
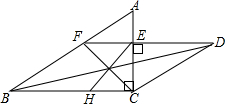 等腰直角△ABC与等腰直角△CDE如图放置,∠ACB=90°,CA=CB,∠CED=90°,EC=ED,点G是BD的中点,连接EG且延长交BC于H,连接CG且延长AB于F,连接EF.
等腰直角△ABC与等腰直角△CDE如图放置,∠ACB=90°,CA=CB,∠CED=90°,EC=ED,点G是BD的中点,连接EG且延长交BC于H,连接CG且延长AB于F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com