
| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 首先根据二次根式有意义得1-x≥0,且x-$\frac{1}{2}$≥0,从而得到$\frac{1}{2}$≤x≤1.然后等式两边分别平方后得到y2=$\frac{1}{2}$+2$\sqrt{-{x}^{2}+\frac{3}{2}x-\frac{1}{2}}$=$\frac{1}{2}$+2$\sqrt{-(x-\frac{3}{4})^{2}+\frac{1}{16}}$,得到当x=$\frac{3}{4}$时,y2取到最大值1,故a=1.当x=$\frac{1}{2}$或1时,y2取到最小值$\frac{1}{2}$,故b=$\frac{\sqrt{2}}{2}$,从而求得代数式的值.
解答 解:由1-x≥0,且x-$\frac{1}{2}$≥0,得$\frac{1}{2}$≤x≤1.
y2=$\frac{1}{2}$+2$\sqrt{-{x}^{2}+\frac{3}{2}x-\frac{1}{2}}$=$\frac{1}{2}$+2$\sqrt{-(x-\frac{3}{4})^{2}+\frac{1}{16}}$.
由于$\frac{1}{2}$<$\frac{3}{4}$<1,
所以当x=$\frac{3}{4}$时,y2取到最大值1,故a=1.
当x=$\frac{1}{2}$或1时,y2取到最小值$\frac{1}{2}$,故b=$\frac{\sqrt{2}}{2}$.
所以:a2+b2=$\frac{3}{2}$=1.5.
故选B.
点评 本题考查了无理函数的最值,特别是确定自变量的取值范围是解答本题的关键,将题目中的等式两边平方是解决无理函数的一种重要方法,难度偏大.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
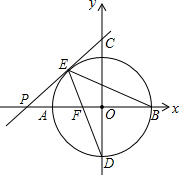 ⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8
⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8查看答案和解析>>
科目:初中数学 来源: 题型:解答题
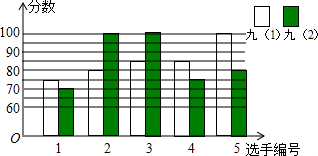
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1) | 85 | 85 | 85 |
| 九(2) | 85 | 80 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴 | |
| B. | 关于某条直线对称的两个图形全等 | |
| C. | 若两个图形沿某条直线对折后能够完全重合,我们称两个图形成轴对称 | |
| D. | 全等的三角形一定关于某条直线对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com