
【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与![]() 轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
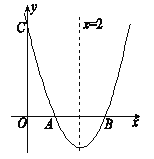
(1) 求抛物线的函数表达式;
(2) 如果抛物线的对称轴上存在一点P,使得△APC周长的最小,求此时△APC周长.
(3) 设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,求点D的坐标.(直接写出结果)
【答案】(1) y=x2-4x+3;(2) ![]() .(3) D的坐标为:(2,-1).
.(3) D的坐标为:(2,-1).
【解析】
试题分析:(1)根据抛物线对称轴的定义易求A(1,0),B(3,0).所以1、3是关于x的一元二次方程x2+bx+c=0的两根.由韦达定理易求b、c的值;
(2)如图,连接AC、BC,BC交对称轴于点P,连接PA.根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可;
(3)如图2,点D是抛物线的顶点,所以根据抛物线解析式利用顶点坐标公式即可求得点D的坐标.
试题解析:(1)∵AB=2,对称轴为直线x=2.
∴点A的坐标是(1,0),点B的坐标是(3,0).
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1、3是关于x的一元二次方程x2+bx+c=0的两根.
由韦达定理,得
1+3=-b,1×3=c,
∴b=-4,c=3,
∴抛物线的函数表达式为y=x2-4x+3;
(2)连接AC、BC,BC交对称轴于点P,连接PA.
由(1)知抛物线的函数表达式为y=x2-4x+3,A(1,0),B(3,0),
∴C(0,3),
∴BC=![]() ,AC=
,AC=![]() .
.
∵点A、B关于对称轴x=2对称,
∴PA=PB,
∴PA+PC=PB+PC.
此时,PB+PC=BC.
∴点P在对称轴上运动时,(PA+PC)的最小值等于BC.
∴△APC的周长的最小值=AC+AP+PC=AC+BC=![]() .
.
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线y=x2-4x+3的顶点坐标,即(2,-1),
当E、D点在x轴的上方,即DE∥AB,AE=AB=BD=DE=2,此时不合题意,
故点D的坐标为:(2,-1).
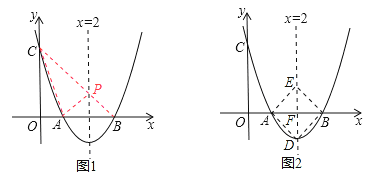


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A. 经过两点有且只有一条直线 B. 平行四边形的对角线相等
C. 两腰相等的梯形叫做等腰梯形 D. 圆的切线垂直于经过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
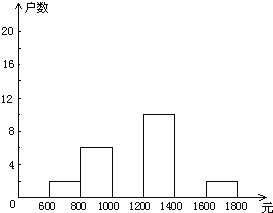
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).

(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式和∠ABC的度数;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com