Question

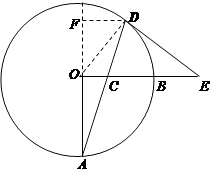
【题目】如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连结AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA＝8．

（1）求证：∠ECD＝∠EDC；
（2）若tanA＝ ，求DE长；
（3）当∠A从15°增大到30°的过程中，求弦AD在圆内扫过的面积．

Answer 1

【答案】
（1）

证明：连结OD，

∵DE是⊙O的切线，∴∠EDC＋∠ODA＝90°，

又∵OA⊥OB，∴∠ACO＋∠A＝90°，

∵OA＝OD，∴∠ODA＝∠A，∴∠EDC＝∠ACO，

又∵∠ECD＝∠ACO，∴∠ECD＝∠EDC．

（2）

解：∵tanA＝ ，∴ ，∴OC＝2，

设DE＝x，∵∠ECD＝∠EDC，∴CE＝x，∴OE＝2＋x．

∵∠ODE＝90°，∴OD2＋DE2＝OE2，

∴82＋x 2＝（2＋x）2，x＝15，∴DE＝CE＝15．

（3）

解：过点D作AO的垂线，交AO的延长于F，

当 时，则 ，DF＝4，

当 时， ，DF＝4 ，

，

【解析】（1）运用切线的性质以及对顶角相等，角的等量代换可证得；（2）由tanA＝ ，可解出OC，由（1）得∠ECD＝∠EDC ， 等角对等边，则EC=DE，由勾股定理得OD2＋DE2＝OE2 ， 构造方程解出DE的长；（3）分别求出 和 时，弓形ABD的面积，再用前者减去后者即可得到答案.