
【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE,若点A到CE的距离为17,则CE= . 
【答案】12或5
【解析】当CE>DE时,
过点A作AF⊥CE,过点D作DG⊥AF,连接AC,则AF=17,
CF= ![]() =7.
=7.
∵AF⊥CE,DG⊥AF,DE⊥CE,
∴四边形DEGF是矩形,
∴∠EDG=90°,
则∠CDE+∠CDG=90°,
又∵∠ADG+∠CDG=90°,
∴∠CDE=∠ADG,
又∵AD=CD,∠AGD=∠CED=90°,
∴△AGD≌△CED,
∴GD=ED,
∴矩形DEFG是正方形,
∴FG=DE=EF,
设FG=DE=EF=x,
由勾股定理得CE2+DE2=CD2 ,
则(7+x)2+x2=132,
解得x=5,
则CE=7=5=12;
当DE>CE时,同理可得CE=5.
故答案为12可5.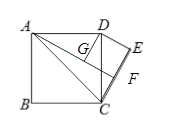
需要分类讨论DE与CE的长度大小;再作如图所示的图,易求得CF的长,再通过证明△AGD≌△CED,最后得到FG=DE=EF,由勾股定理构造方程解出DE的长即可.


科目:初中数学 来源: 题型:
【题目】用适当方法解下列方程
(1)x(x+4)=8x+12
(2)(x+3)2=25(x﹣1)2
(3)(x+1)(x+8)=﹣12
(4)x4﹣x2﹣6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2 ![]() ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O直径,以OA为直径作⊙M.过B作⊙M得切线BC,切点为C,交⊙O于E. 
(1)在图中过点B作⊙M作另一条切线BD,切点为点D(用尺规作图,保留作图痕迹,不写作法,不用证明);
(2)证明:∠EAC=∠OCB;
(3)若AB=4,在图2中过O作OP⊥AB交⊙O于P,交⊙M的切线BD于N,求BN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=3m.

(1)求∠DAC的度数;
(2)求这棵大树折断前的高度?(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA= ![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为 . 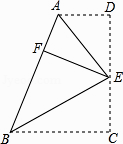
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )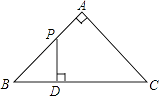
A.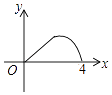
B.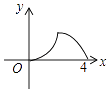
C.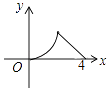
D.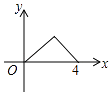
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com