
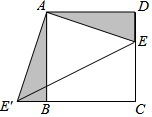
 如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.
如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.分析 (1)根据正方形的性质得AD=AB,∠DAB=90°,∠D=90°,在Rt△ADE中利用勾股定理可计算出AE=$\sqrt{10}$,由于△ADE顺时针旋转90°,得△ABE′,
根据旋转的性质得∠EAE′=∠DAB=90°,E′A=EA,则可判断△EAE′为等腰直角三角形;
(2)根据等腰直角三角形的性质得到EE′=$\sqrt{2}$EA,然后根据勾股定理即可得到结论.
解答 解:(1)等腰直角三角形.
理由:∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,∠D=90°,
在Rt△ADE中,DE=1,AD=3,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{10}$,
∵△ADE顺时针旋转90°,得△ABE′,
∴∠EAE′=∠DAB=90°,E′A=EA,
∴△EAE′为等腰直角三角形;
故答案为:等腰直角;
(2)∵△EAE′为等腰直角三角形,
∴EE′=$\sqrt{A{E}^{2}+AE{′}^{2}}$=2$\sqrt{5}$,
∵S△AEE'=$\frac{1}{2}$AE•AE′=$\frac{1}{2}$EE′•AH,
∴EE'•AH=AE•AE',
即 2$\sqrt{5}$•AH=$\sqrt{10}$•$\sqrt{10}$,
∴AH=$\sqrt{5}$.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质和等腰直角三角形的判定与性质.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{12}$(x-4)2+3,由此可知铅球推出的距离是多少米?
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{12}$(x-4)2+3,由此可知铅球推出的距离是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com