
 《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )| A. | 5步 | B. | 6步 | C. | 8步 | D. | 10步 |
分析 由勾股定理可求得斜边长,分别连接圆心和三个切点,设内切圆的半径为r,利用面积相等可得到关于r的方程,可求得内切圆的半径,则可求得内切圆的直径.
解答  解:
解:
如图,在Rt△ABC中,AC=8,BC=15,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=17,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×8×15=60,
设内切圆的圆心为O,分别连接圆心和三个切点,及OA、OB、OC,
设内切圆的半径为r,
∴S△ABC=S△AOB+S△BOC+S△AOC=$\frac{1}{2}$×r(AB+BC+AC)=20r,
∴20r=60,解得r=3,
∴内切圆的直径为6步,
故选B.
点评 本题主要考查三角形的内切圆,连接圆心和切点,把三角形的面积分成三个三个角形的面积得到关于r的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
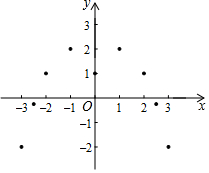 某“数学兴趣小组”根据学习函数的经验,对函数y=-x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整:
某“数学兴趣小组”根据学习函数的经验,对函数y=-x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整:| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | m | 2 | 1 | 2 | 1 | -$\frac{1}{4}$ | -2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
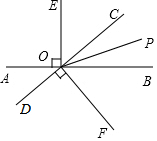 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com