
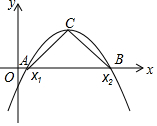
 如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1<x2.
如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1<x2.分析 (1)由题意1-m<0,解不等式即可.
(2)根据抛物线的对称轴列出方程即可解决问题.
(3)由(1-m)x2+4x-3=0,有x1+x2=$\frac{4}{m-1}$,x1•x2=$\frac{3}{m-1}$,推出|AB|=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{4}{m-1})^{2}-\frac{12}{m-1}}$,又因为-$\frac{b}{2a}$=$\frac{2}{m-1}$,$\frac{4ac-{b}^{2}}{4a}$=$\frac{3m-7}{1-m}$,所以顶点C的坐标为($\frac{2}{m-1}$,$\frac{3m-7}{1-m}$),根据△ABC是等腰直角三角形,可得|$\frac{3m-7}{1-m}$|=$\frac{1}{2}$$\sqrt{(\frac{4}{m-1})^{2}-\frac{12}{m-1}}$,解方程即可.
解答 解:(1)由题意1-m<0,即m>1.
(2)由题意-$\frac{4}{2(1-m)}$=5,解得m=$\frac{7}{5}$,
∴抛物线的解析式为y=-$\frac{2}{5}$x2+4x-3.
(3)由(1-m)x2+4x-3=0,有x1+x2=$\frac{4}{m-1}$,x1•x2=$\frac{3}{m-1}$,
∴|AB|=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{4}{m-1})^{2}-\frac{12}{m-1}}$,
又∵-$\frac{b}{2a}$=$\frac{2}{m-1}$,$\frac{4ac-{b}^{2}}{4a}$=$\frac{3m-7}{1-m}$,
∴顶点C的坐标为($\frac{2}{m-1}$,$\frac{3m-7}{1-m}$),
∵△ABC是等腰直角三角形,
∴|$\frac{3m-7}{1-m}$|=$\frac{1}{2}$$\sqrt{(\frac{4}{m-1})^{2}-\frac{12}{m-1}}$,
解得m=2或$\frac{7}{3}$.
∴抛物线的解析式为y=-x2+4x-3或y=-$\frac{4}{3}$x2+4x-3.
点评 本题考查了二次函数综合题,涉及函数与方程的关系、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用方程思想思考问题,属于中考常考题型.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
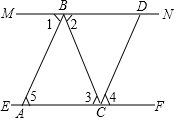 如图,MN、EF是两面互相平行的镜面,光线AB照射到镜面MN上,反射光线为BC,光线BC又经镜面EF反射后,反射光线为CD,已知入射光线与反射光线和镜面所成的角相等(即∠1=∠2,∠3=∠4),试说明AB∥CD,根据下列解答填空(理由或数学式).
如图,MN、EF是两面互相平行的镜面,光线AB照射到镜面MN上,反射光线为BC,光线BC又经镜面EF反射后,反射光线为CD,已知入射光线与反射光线和镜面所成的角相等(即∠1=∠2,∠3=∠4),试说明AB∥CD,根据下列解答填空(理由或数学式).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
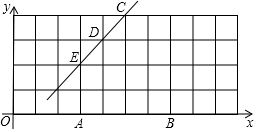 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好,己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,如图建立直角坐标系,则:
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好,己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,如图建立直角坐标系,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com