解:(1)原式=4m
2+4n+2n-4m
2
=6n;
(2)原式=5ab
2-a
2b-2a
2b+6ab
2
=-3a
2b+11ab
2;
(3)∵(x+1)
2+|y-2|=0,
∴x+1=0或y-2=0,
解得:x=-1,y=2,
原式=

x-2x+

y-

x+

y
=y-3x
=2+3
=5;
(4)(2x
2+ax-y+1)-(2bx
2-3x+5y-4)
=2x
2+ax-y+1-2bx
2+3x-5y+4
=(2-2b)x
2+(a+3)x-6y+5,
∵此多项式与x的取值无关,
∴2-2b=0,且a+3=0,
解得:a=-3,b=1,
则原式=

a
3-2b
2-

a
3+3b
2
=

a
3+b
2
=

×(-27)+3
=-

.
分析:(1)原式利用去括号法则去括号后,合并同类项即可得到结果;
(2)原式利用去括号法则去括号后,合并同类项即可得到结果;
(3)由已知两非负数之和为0,两非负数分别为0求出x与y的值,将所求式子利用去括号法则去括号后,合并得到最简结果,把x与y的值代入计算,即可求出值;
(4)将已知代数式去括号合并后,根据代数式的值与字母x所取的值无关,求出a与b的值,将所求式子去括号合并后,把a与b的值代入计算,即可求出值.
点评:此题考查了整式的加减-化简求值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.

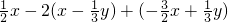 的值.
的值.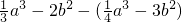 的值.
的值. x-2x+
x-2x+ y-
y- x+
x+ y
y a3-2b2-
a3-2b2- a3+3b2
a3+3b2 a3+b2
a3+b2 ×(-27)+3
×(-27)+3 .
.
