
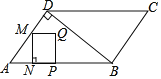
【题目】如图,在ABCD中,对角线DB⊥AD,BC=3,BD=4.点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动(点P不与点A,B重合),点N为AP的中点,过点N作NM⊥AB交折线AD﹣DC于点M,以MN,NP为边作矩形MNPQ.设点P运动的时间为t(s).
(1)求线段PQ的长;(用含t的代数式表示)
(2)求点Q落在BD上时t的值;
(3)设矩形MNPQ与△ABD重叠部分图形的面积为S平方单位,当此重叠部分为四边形时,求S与t之间的函数关系式;
(4)若点D关于直线AB的对称点为点D',点B关于直线PQ的对称点为点B',请直接写出直线B'D'与ABCD各边所在直线平行或垂直的所有t的值.
【答案】(1)当0<t≤![]() 时,PQ=
时,PQ=![]() t;当
t;当![]() <t<
<t<![]() 时,PQ=
时,PQ=![]() ;(2)t=
;(2)t=![]() ;(3)当0<t<
;(3)当0<t<![]() 时, S=
时, S=![]() t2,当
t2,当![]() ≤t<
≤t<![]() 时,S=﹣
时,S=﹣![]() t2+
t2+![]() t;(4)
t;(4)![]() s或
s或![]() s或
s或![]() s.
s.
【解析】
(1)①如图1中,作DH⊥AB于H.解直角三角形求出DH,AH,分两种情形:当0<t≤![]() 时,当
时,当![]() <t<
<t<![]() 时,分别求解即可;
时,分别求解即可;
(2)解直角三角形求出AM,DM(用t表示),根据AM+DM=3,构建方程即可解决问题;
(3)分两种情形①当0<t<![]() 时,如图1中,重叠部分是矩形MNPQ.②如图4中,当
时,如图1中,重叠部分是矩形MNPQ.②如图4中,当![]() ≤t<
≤t<![]() 时,重叠部分是四边形EFNP,分别求解即可;
时,重叠部分是四边形EFNP,分别求解即可;
(4)分三种情形:①如图5中,当D,P,Q共线时,B′D′⊥AD.②如图6中,当B′在直线DD′上时,B′D′⊥AB.③如图7中,当AH=HB′=![]() 时,B′D′∥AD,分别求解即可解决问题.
时,B′D′∥AD,分别求解即可解决问题.
解:(1)①如图1中,作DH⊥AB于H.
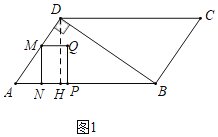
在Rt△ABD中,∵AD=3,BD=4,
∴AB=![]() =
=![]() =5,
=5,
∵S△ABD=![]() ADDB=
ADDB=![]() ABDH,
ABDH,
∴DH=![]() =
=![]() ,
,
∴AH=![]() =
=![]() ,
,
∴点N从点A到点H的时间为:2AH÷2=![]() s,点P从A到B的时间为:AB÷2=
s,点P从A到B的时间为:AB÷2=![]() s
s
∴当0<t≤![]() 时,
时,
由题意可知AP=2t
AN=AP÷2=t
∵MN∥DH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴MN=![]() t,
t,
∵四边形MNPQ是矩形,
∴PQ=MN=![]() t.
t.
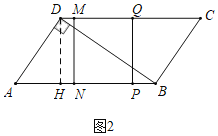
②如图2中,当![]() <t<
<t<![]() 时,PQ=DH=
时,PQ=DH=![]() .
.
综上所述:当0<t≤![]() 时,PQ=
时,PQ=![]() t;当
t;当![]() <t<
<t<![]() 时,PQ=
时,PQ=![]() ;
;
(2)如图3中,当点Q落在BD上时,
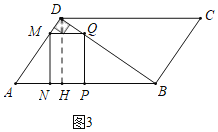
在Rt△AMN中,∵AN=NP=t,cosA=![]() =
=![]() =
=![]() ,
,
∴AM=![]() t,
t,
在Rt△DQM中,∵MQ=PN=t,sin∠DQM=sin∠ABD=![]() =
=![]() ,
,
∴DM=![]() t,
t,
∵AM+DM=3,
∴![]() t+
t+![]() t=3,
t=3,
∴t=![]() .
.
(3)①当0<t<![]() 时,如图1中,重叠部分是矩形MNPQ,S=PNMN=t
时,如图1中,重叠部分是矩形MNPQ,S=PNMN=t![]() t=
t=![]() t2.
t2.

②如图4中,当![]() ≤t<
≤t<![]() 时,重叠部分是四边形EFNP,
时,重叠部分是四边形EFNP,
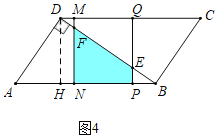
∵AN=t,AP=2t
∴BN=5-t,BP=5-2t
∵tan∠DBH=![]()
∴PE=![]() BP=
BP=![]() (5-2t),FN=
(5-2t),FN=![]() BN=
BN=![]() (5-t)
(5-t)
∴S=S△BNF﹣S△PBE=![]() ×
×![]() (5﹣t)2﹣
(5﹣t)2﹣![]() ×
×![]() (5﹣2t)2=﹣
(5﹣2t)2=﹣![]() t2+
t2+![]() t.
t.
(4)①如图5中,当D,P,Q共线时,B′D′⊥AD.理由如下

由对称性可知:BP= B′P,DP= D′P,
∵∠BPD=∠B′PD′
∴△BPD≌△B′PD′
∴∠DBA=∠B′
∴DB∥B′D′
∴B′D′⊥AD
此时2t=![]() ,t=
,t=![]() .
.
②如图6中,当B′在直线DD′上时,易知B′D′⊥AB,
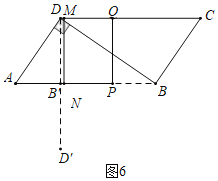
此时∵AB′+2BP=AB,
∴![]() +2(5﹣2t)=5,
+2(5﹣2t)=5,
∴t=![]() .
.
③如图7中,当AH=HB′=![]() 时,B′D′∥AD,理由如下
时,B′D′∥AD,理由如下
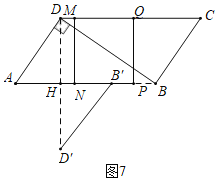
由对称性可知:AH= B′H,DH= D′H,
∵∠AHD=∠B′H D′
∴△AHD≌△B′H D′
∴∠A=∠HB′D′
∴B′D′∥AD
此时2AH+2BP=5
∴2×![]() +2(5﹣2t)=5,
+2(5﹣2t)=5,
∴t=![]() ,
,
综上所述,满足条件的t的值为![]() s或
s或![]() s或
s或![]() s.
s.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是我国运动员在最近六届奥运会上所获奖牌总数情况:
届数 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |
31 | 26 | 18 | 26 | 70 |
数学小组分析了上面的数据,得出这六届奥运会我国奖牌总数的平均数、中位数如表所示:
统计量 | 平均数 | 中位数 |
数值 | 约为71.67 | m |
(1)上表中的中位数m的值为 ;
(2)经过数学小组的讨论,认为由于第29届奥运会在我国北京召开,我国运动员的成绩超常,所以其数据应记为极端数据,在计算平均数时应该去掉,于是计算了另外五属奥运会上我国奖总数的平均数,这个平均数应该是
(3)根据上面提供的信息,预估我国运动员在2020年举行的第32届奥运会上将获得多少枚奖牌,并写出你的预估理由
查看答案和解析>>
科目:初中数学 来源: 题型:
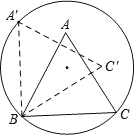
【题目】如图,正△ABC 的边长为 2,顶点 B、C 在半径为![]() 的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
的圆上,顶点 A在圆内,将正△ABC 绕点 B 逆时针旋转,当点 A 第一次落在圆上时,则点 C 运动的路线长为 (结果保留π);若 A 点落在圆上记做第 1 次旋转,将△ABC 绕点 A 逆时针旋转,当点 C 第一次落在圆上记做第 2 次旋转,再绕 C 将△ABC 逆时针旋转,当点 B 第一次落在圆上,记做第 3 次旋转……,若此旋转下去,当△ABC 完成第 2017 次旋转时,BC 边共回到原来位置 次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,下列结论:①
之间,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;其中正确的有( )
;其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
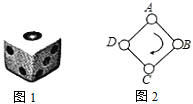
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com