
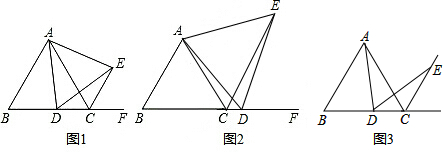
���� ��1�����ݵȱ������ε����ʼ���ʽ�����ʾͿ��Եó���ABD�ա�ACE���Ӷ��ó����ۣ����ݵȱ������ε����ʼ���ʽ�����ʾͿ��Եó���ABD�ա�ACE���Ϳ��Եó�BD=CE���Ϳ��Եó�AC=CE-CD��
��2������Ϊ��CDE���ܳ�=AD+DC+CE���ɣ�1��֤��CE=BD�����ǵõ�CD+CE=BC=2���õ���CDE���ܳ���Сʱ��AD��BC�����AD=$\sqrt{3}$���õ���CDE���ܳ�=2+$\sqrt{3}$��
���ɵ���D��B�˶���C���õ� ��E���˶�·��=��D���˶�·��=2��
��3������D��DF��AC��AB�ڵ�F��ͨ��֤��������ȫ�ȵõ����ۣ�
��� ��1����CD+AC=CE����
�⣺�ߡ�ABC�͡�ADE���ǵȱ������Σ�
��AB=AC=BC��AD=AE����BAC=��DAE=60�㣮
���BAC-��CAD=��DAE-��CAD������BAD=��CAE��
�ڡ�ABD�͡�ACE�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAE}\\{AD=AE}\end{array}\right.$��
���ABD�ա�ACE��SAS����
��BD=CE��
��BC=BD+CD��AC=BC��
��AC=CE+CD��
��2��AC��CE��CD֮����ڵ�������ϵ�ǣ�AC=CE-CD�����ɣ�
�⣺�ߡ�ABC�͡�ADE���ǵȱ������Σ�
��AB=AC=BC��AD=AE����BAC=��DAE=60�㣮
���BAC+��CAD=��DAE+��CAD��
���BAD=��CAE
�ڡ�ABD�͡�ACE�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BA��CAE}\\{AD=AE}\end{array}\right.$
���ABD�ա�ACE��SAS��
��BD=CE
��CE-CD=BD-CD=BC=AC��
��AC=CE-CD��
��2���⣺�١ߡ�CDE���ܳ�=AD+DC+CE��
�ɣ�1��֤��CE=BD��
��CD+CE=BC=2��
���CDE���ܳ���Сʱ��AD��BC��
��BC=2����AD=$\sqrt{3}$��
���CDE���ܳ�=2+$\sqrt{3}$��
�ڡߵ���D��B�˶���C��
���D���˶�·��Ϊ2��
���E����D���˶����˶���
���E���˶�·��=��D���˶�·��=2��
��3���⣺��ͼ3��CE=BD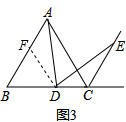 ��
��
����D��DF��AC��AB�ڵ�F��
�ߡ�ABC�ǵȱ������Σ�
���BAC=��ACB=��B=60�㣬
���BFD=��BAC=60�㣬
���BFD�ǵȱ������Σ�
��BF=BD����AB=AC��
��AF=CD��
�ߡ�ADE=60�㣬
���ADB+��CDE=120�㣬
�֡ߡ�B=60�㣬
���ADB+��BAD=120�㣬
���CDE=��BAD��
�֡ߡ�AFD=��DCE=120�㣬
�ڡ�AFD���DCE�У�
$\left\{\begin{array}{l}{��BAD=��CDE}\\{AF=CD}\\{��AFD=��DCE}\end{array}\right.$��
���AFD�ա�DCE��ASA����
��CE=DF��
�֡�DF=BD��
��CE=BD��
���� ���⿼���˵ȱ������ε����ʵ����ã���ʽ�����ʵ����ã�ȫ�������ε��ж������ʵ����ã����ʱ֤��������ȫ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
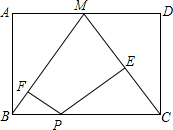 ��ͼ����M�Ǿ���ABCD�ı�AD���е㣬��P��BC���ϵ�һ�����㣬PE��CM��PF��BM������ֱ�E��F��
��ͼ����M�Ǿ���ABCD�ı�AD���е㣬��P��BC���ϵ�һ�����㣬PE��CM��PF��BM������ֱ�E��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
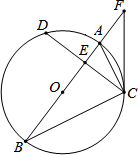 ��ͼ���ڡ�O�У�ֱ��ABƽ����CD��AB��CD�ཻ�ڵ�E������AC��BC����F��BA�ӳ����ϵ�һ�㣬�ҡ�FCA=��B��
��ͼ���ڡ�O�У�ֱ��ABƽ����CD��AB��CD�ཻ�ڵ�E������AC��BC����F��BA�ӳ����ϵ�һ�㣬�ҡ�FCA=��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
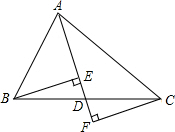 ��ͼ���ڡ�ABC�У���D��BC�ߵ��е㣬�ֱ����B��C��BE��AD�ڵ�E��CF��AD��AD���ӳ����ڵ�F����֤��DE=DF��
��ͼ���ڡ�ABC�У���D��BC�ߵ��е㣬�ֱ����B��C��BE��AD�ڵ�E��CF��AD��AD���ӳ����ڵ�F����֤��DE=DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
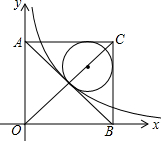 ��ͼ����ƽ��ֱ������ϵ����һ������AOBC������������y=$\frac{k}{x}$����������AOBC�Խ��ߵĽ��㣬�뾶Ϊ��4-2$\sqrt{2}$����Բ�����ڡ�ABC����k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ����һ������AOBC������������y=$\frac{k}{x}$����������AOBC�Խ��ߵĽ��㣬�뾶Ϊ��4-2$\sqrt{2}$����Բ�����ڡ�ABC����k��ֵΪ��������| A�� | 4$\sqrt{2}$ | B�� | 4 | C�� | 2$\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com