
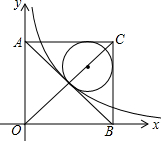
 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
分析 根据正方形的性质得出AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,进而根据半径为(4-2$\sqrt{2}$)的圆内切于△ABC,得出CD的长,从而得出DO的长,再利用勾股定理得出DN的长进而得出k的值.
解答 解:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N;
设圆心为Q,切点为H、E,连接QH、QE.
∵在正方形AOBC中,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形,
∵半径为(4-2$\sqrt{2}$)的圆内切于△ABC,
∴DO=CD,
∵HQ2+HC2=QC2,
∴2HQ2=QC2=2×(4-2$\sqrt{2}$)2,
∴QC2=48-32$\sqrt{2}$=(4$\sqrt{2}$-4)2,
∴QC=4$\sqrt{2}$-4,
∴CD=4$\sqrt{2}$-4+(4-2$\sqrt{2}$)=2$\sqrt{2}$,
∴DO=2$\sqrt{2}$,
∵NO2+DN2=DO2=(2$\sqrt{2}$)2=8,
∴2NO2=8,
∴NO2=4,
∴DN×NO=4,
即:xy=k=4.
故选B.
点评 本题考查了反比例函数综合题,涉及正方形的性质以及三角形内切圆的性质以及待定系数法求反比例函数解析式,根据已知求出CD的长度,进而得出DN×NO=4是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
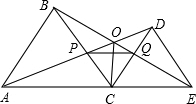 如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.
如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 阴天会下雨是必然事件 | |
| B. | 若关于x的一元二次方程kx2-2x-1=0有实数根,则k≥-1 | |
| C. | 在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k | |
| D. | 多边形的外角和等于360° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7和10 | B. | 10和12 | C. | 9和10 | D. | 10和10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
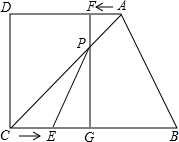 如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.
如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com