
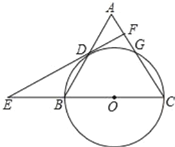
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
【答案】①③④
【解析】
连接OD,BG,CD,如图,利用切线的性质得到OD⊥DF,再利用圆周角定理和等腰三角形的性质证明OD∥AC,则可对①进行判断;利用OB=![]() BC=5,BD=6可对②进行判断;利用勾股定理计算出CD=8,则可计算出
BC=5,BD=6可对②进行判断;利用勾股定理计算出CD=8,则可计算出![]() ABC的面积,从而可对③进行判断;利用面积法计算出BG=
ABC的面积,从而可对③进行判断;利用面积法计算出BG=![]() ,则cos∠CBG=
,则cos∠CBG=![]() ,然后证明∠E=∠CBG,从而可对④进行判断.
,然后证明∠E=∠CBG,从而可对④进行判断.
解:连接OD,BG,CD,如图,
∵DF为切线,
∴OD⊥DF,
∵BC为直径,
∴∠BDC=90°,
∵CA=CB,
∴CD平分AB,即AD=BD=6,
而OB=OC,
∴OD为![]() ABC的中位线,
ABC的中位线,
∴OD∥AC,
∴DF⊥AC,所以①正确;
∵OB=![]() BC=5,BD=6,
BC=5,BD=6,
∴OD≠BD,所以②错误;
在Rt![]() BCD中,CD=
BCD中,CD=![]() =8,
=8,
∴S△ABC=![]() CDAB=
CDAB=![]() ×8×12=48,所以③正确;
×8×12=48,所以③正确;
∵BC为直径,
∴∠BGC=90°,
∴S△ABC=![]() BGAC=48,
BGAC=48,
∴BG=![]() ,
,
∴cos∠CBG=![]() =
=![]() =
=![]() ,
,
∵BG⊥AC,EF⊥AC,
∴BG∥EF,
∴∠E=∠CBG,
∴cos∠E=![]() ,所以④正确.
,所以④正确.
故答案为:①③④.



 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
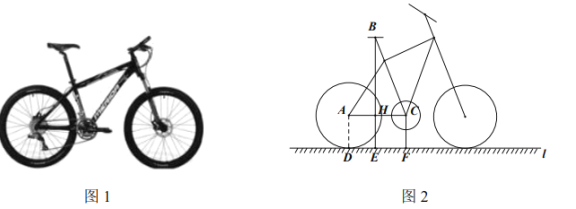
查看答案和解析>>
科目:初中数学 来源: 题型:
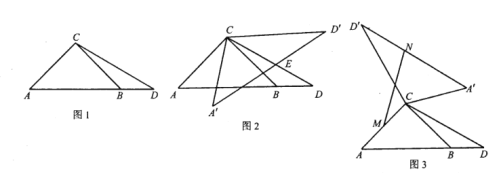
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边的延长线上,且
边的延长线上,且![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )得到
)得到![]() .
.
①若![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的长度;
的长度;
②连接![]() ,
,![]() ,若旋转过程中
,若旋转过程中![]() 时,求满足条件的
时,求满足条件的![]() 的度数.
的度数.
(3)如图3,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )得到
)得到![]() ,若点
,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点,直接写出旋转过程中,线段
上任意一点,直接写出旋转过程中,线段![]() 长度的取值范围为______.
长度的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若直角△ABC的两直角边AB、AC的长是该方程的两个实数根,斜边BC的长为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
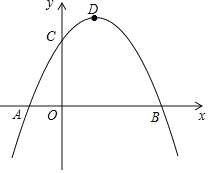
【题目】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;
(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |

已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
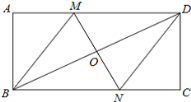
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 在抛物线上,将抛物线
在抛物线上,将抛物线![]() 在点
在点![]() 右侧的部分沿着直线
右侧的部分沿着直线![]() 翻折,翻折后的图象与原抛物线剩余部分合称为图象
翻折,翻折后的图象与原抛物线剩余部分合称为图象![]() .
.
(1)当![]() 时,
时,
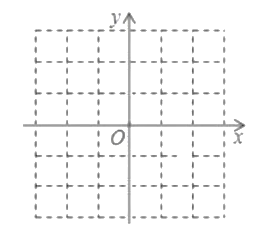
①在如图的平面直角坐标系中画出图象![]() ;
;
②直接写出图象![]() 对应函数的表达式;
对应函数的表达式;
③当![]() 时,图象
时,图象![]() 对应函数的最小值为
对应函数的最小值为![]() 求
求![]() 的取值范围.
的取值范围.
(2)当![]() 时,直接写出图象
时,直接写出图象![]() 对应函数
对应函数![]() 随
随![]() 增大而减小时
增大而减小时![]() 的取值范围.
的取值范围.
(3)若图象![]() 上有且只有三个点到直线
上有且只有三个点到直线![]() 的距离为
的距离为![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com