
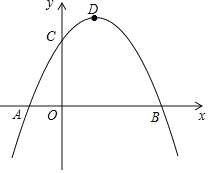
【题目】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;
(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)见解析;(3)见解析.
x+2;(2)见解析;(3)见解析.
【解析】
(1)由OC与OB的长,确定出B与C的坐标,再由A坐标,利用待定系数法确定出抛物线解析式即可;
(2)分三种情况讨论:当四边形CBPD是平行四边形;当四边形BCPD是平行四边形;四边形BDCP是平行四边形时,利用平移规律确定出P坐标即可;
(3)由B与C坐标确定出直线BC解析式,求出与直线BC平行且与抛物线只有一个交点时交点坐标,确定出交点与直线BC解析式,进而确定出另一条与直线BC平行且与BC距离相等的直线解析式,确定出所求M坐标,且求出定值S的值即可.
(1)由OC=2,OB=3,得到B(3,0),C(0,2),
设抛物线解析式为y=a(x+1)(x﹣3),
把C(0,2)代入得:2=﹣3a,即a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+1)(x﹣3)=﹣
(x+1)(x﹣3)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)抛物线y=﹣![]() (x+1)(x﹣3)=﹣
(x+1)(x﹣3)=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴D(1,![]() ),
),
当四边形CBPD是平行四边形时,由B(3,0),C(0,2),得到P(4,![]() );
);
当四边形CDBP是平行四边形时,由B(3,0),C(0,2),得到P(2,﹣![]() );
);
当四边形BCPD是平行四边形时,由B(3,0),C(0,2),得到P(﹣2,![]() );
);
(3)设直线BC解析式为y=kx+b,
把B(3,0),C(0,2)代入得:![]() ,
,
解得: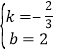 ,
,
∴y=﹣![]() x+2,
x+2,
设与直线BC平行的解析式为y=﹣![]() x+b,
x+b,
联立得: ,
,
消去y得:2x2﹣6x+3b﹣6=0,
当直线与抛物线只有一个公共点时,△=36﹣8(3b﹣6)=0,
解得:b=![]() ,即y=﹣
,即y=﹣![]() x+
x+![]() ,
,
此时交点M1坐标为(![]() ,
,![]() );
);
可得出两平行线间的距离为![]() ,
,
同理可得另一条与BC平行且平行线间的距离为![]() 的直线方程为y=﹣
的直线方程为y=﹣![]() x+
x+![]() ,
,
联立解得:M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),
),
此时S=1.



 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=![]() (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣![]() t2+5t﹣
t2+5t﹣![]() )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣![]() t2+3t﹣
t2+3t﹣![]() )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣![]() x2+bx+c的顶点.
x2+bx+c的顶点.
①当点P在双曲线y=![]() 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=![]() 没有公共点;
没有公共点;
②当抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据爱因斯坦的相对论,当地面上经过1秒钟时,宇宙飞船内只经过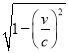 秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论.
秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
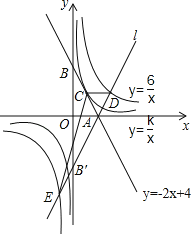
【题目】如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y=![]() 的图象有唯一的公共点C.
的图象有唯一的公共点C.
(1)求k的值及C点坐标;
(2)直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y=![]() 交于D、E两点,求△CDE的面积.
交于D、E两点,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
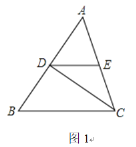
【题目】已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC,
(1)如果点E是边AC的中点,AC=5cm,求DE的长;
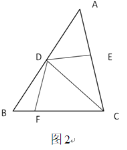
(2)如图2,若DE平分∠ADC,在BC边上取点F,使∠DFC=60°,若BC=7,BF=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
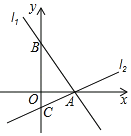
【题目】如图,过点A(4,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=2![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为20,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与正比例函数![]() 的图象交于点
的图象交于点![]() ,与y轴交于点
,与y轴交于点![]() .点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足
.点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作长方形PDEF,满足![]() 轴,且
轴,且![]() ,
,![]() .
.
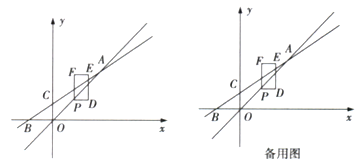
(1)求k的值及直线AB的函数表达式,并判定![]() 时,点E是否落在直线AB上;
时,点E是否落在直线AB上;
(2)在点P运动的过程中,当点F落在直线AB上时,求t的值;
(3)在点P运动的过程中,若长方形PDEF与直线AB有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>![]() 时,y<0
时,y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com