练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】关于一次函数y=﹣2x+3，下列结论正确的是（　　）

    A. 图象过点（1，﹣1） B. 图象经过一、二、三象限

    C. y随x的增大而增大 D. 当x＞时，y＜0

    【答案】D

    【解析】A、把点的坐标代入关系式，检验是否成立；B、根据系数的性质判断，或画出草图判断；C、根据一次项系数判断；D、可根据函数图象判断，亦可解不等式求解．

    解：A、当x=1时，y=1．所以图象不过（1，-1），故错误；
    B、∵-2＜0，3＞0，∴图象过一、二、四象限，故错误；
    C、∵-2＜0，∴y随x的增大而减小，故错误；
    D、画出草图．
    ∵当x＞时，图象在x轴下方，∴y＜0，故正确．
    故选D．

    “点睛”本题主要考查了一次函数的性质以及一次函数与方程、不等式的关系．常采用数形结合的方法求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

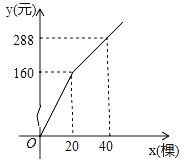
    【题目】 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

    （1）求y与x的函数关系式；

    （2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

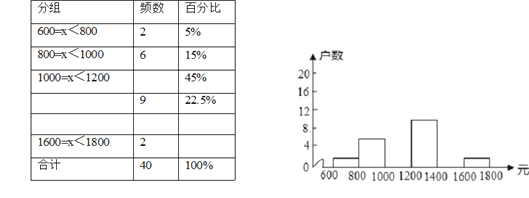
    【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况．他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．

    根据以上提供的信息，解答下列问题：

    （1）补全频数分布表．

    （2）补全频数分布直方图．

    （3）绘制相应的频数分布折线图．

    （4）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的弦CD与直径AB垂直于F，点E在CD上，且AE=CE．

    （1）求证：CA2=CE CD；

    （2）已知CA=5，EC=3，求sin∠EAF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

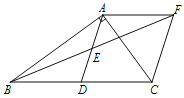
    【题目】已知：在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A做AF∥BC交BE的延长线于点F．

    （1）求证：△AEF≌△DEB；

    （2）证明四边形ADCF是菱形；若AC=4，AB=5，求菱形ADCF的面积．

    （3）当△ABC满足什么条件时，四边形ADCF是正方形，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

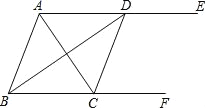
    【题目】如图，AE∥BF，AC平分∠BAE，交BF于点C，BD平分∠ABC，交AE于点D，连接CD．

    （1）求证：四边形ABCD是菱形；

    （2）若AB=5，AC=6，求AE，BF之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明购买A，B两种商品，每次购买同一种商品的单价相同，具体信息如下表：

    次数

    购买数量（件

    购买总费用（元

    A

    B

    第一次

    2

    1

    55

    第二次

    1

    3

    65

    根据以上信息解答下列问题：

    （1）求A，B两种商品的单价；

    （2）若第三次购买这两种商品共12件，且A种商品的数量不少于B种商品数量的2倍，请设计出最省钱的购买方案，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＋∠2﹦180°,∠3﹦∠B，则DE∥BC，下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容．

    证明：

    ∵∠1＋∠2﹦180（已知），

    ∠1﹦∠4 （_________________），

    ∴∠2﹢_____﹦180°.

    ∴EH∥AB（___________________________________）．

    ∴∠B﹦∠EHC（________________________________）．

    ∵∠3﹦∠B（已知）

    ∴ ∠3﹦∠EHC（____________________）．

    ∴ DE∥BC（__________________________________）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：(1)当线段AB平行于投影面P时，它的正投影是线段A1B1，线段与它的投影的大小关系为AB

    ___A1B1；

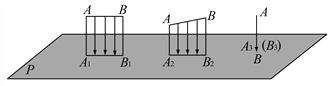
    (2)当线段AB倾斜于投影面P时，它的正投影是线段A2B2，线段与它的投影的大小关系为AB___A2B2；

    (3)当线段AB垂直于投影面P时，它的正投影是______.

    查看答案和解析>>

    同步练习册答案