
【题目】已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;若AC=4,AB=5,求菱形ADCF的面积.
(3)当△ABC满足什么条件时,四边形ADCF是正方形,请说明理由.
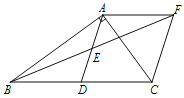
【答案】(1)见解析;(2)菱形ADCF的面积=10;(3)当AB=AC时,四边形ADCF是正方形,理由见解析.
【解析】
(1)根据AAS证△AFE≌△DBE;
(2)利用全等三角形的对应边相等得到AF=BD.证出四边形ADCF是平行四边形,再由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出四边形ADCF是菱形;由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论;
(3)当AB=AC时和D是BC的中点可得:AD⊥BC,从而得出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AEF和△DEB中,
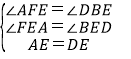 ,
,
∴△AEF≌△DEB(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
连接DF,如图所示:
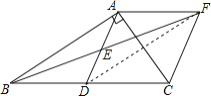
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴菱形ADCF的面积=![]() ACDF=
ACDF=![]() ×4×5=10.
×4×5=10.
(3)当AB=AC时,四边形ADCF是正方形,
理由:∵AB=AC,D是BC的中点,
∴ AD⊥BC,
又∵四边形ADCF是菱形,
∴菱形ADCF是正方形.


科目:初中数学 来源: 题型:
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况,他在学校中随机抽取了400名学生进行调查统计并制成如下图表,
|
|
请根据图表提供的信息解答下列问题:
(1)a =__________,b =__________;
(2)补全频数分布直方图;
(3)若全校共有3000名学生,请你估计该校每周零花钱超过50元的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.
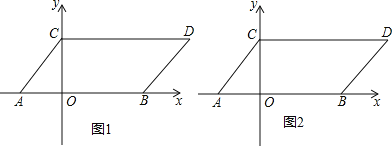
(1)点C的坐标为 ,点D的坐标为 ,四边形ABDC的面积为 .
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>![]() 时,y<0
时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小聪去某文具商店购买学习用品的数据如下表(因污损导致部分数据无法识别):
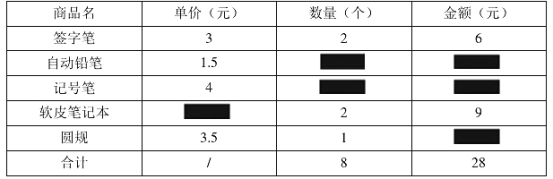
仔细观察表格中数据之间的关系,解决下列问题:
(1)这家文具商店软面笔记本的单价是________元/本,小聪购买圆规共花费______元;
(2)小聪购买了自动铅笔、记号笔各几支?
(3)若小明也在同一家文具店购买了软面笔记本和自动铅笔两种文具,已知他恰好花费12元,请你对小明购买的软面笔记本和自动铅笔数量的可能性进行分析。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com