
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

科目:初中数学 来源: 题型:
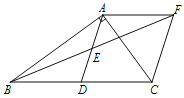
【题目】已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;若AC=4,AB=5,求菱形ADCF的面积.
(3)当△ABC满足什么条件时,四边形ADCF是正方形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
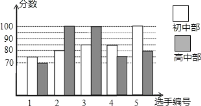
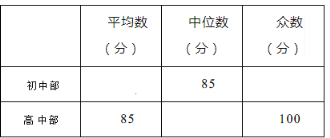
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
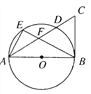
【题目】如图所示,AB是00的直径,BC是⊙O的切线,连接AC,交⊙0于D,E为弧AD上一点,连接AE,BE交AC于点F且![]() ,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=
,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;
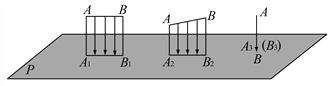
(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
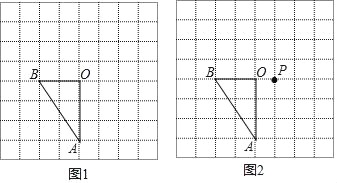
【题目】在8×8的正方形网格中,有一个Rt△AOB,点O是直角顶点,点O、A、B分别在网格中小正方形的顶点上,请按照下面要求在所给的网格中画图.
(1)在图1中,将△AOB先向右平移3个单位,再向上平移2个单位,得到△A1O1B1,画出平移后的△A1O1B1;(其中点A、O、B的对应点分别为点A1,O1,B1)
(2)在图2中,△AOB与△A2O2B2是关于点P对称的图形,画出△A2O2B2,连接BA2,并直接写出tan∠A2BO的值.(其中A,O,B的对应点分别为点A2,O2,B2)
查看答案和解析>>
科目:初中数学 来源: 题型:
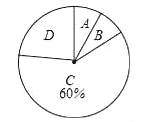
【题目】今年10月,某公司随机抽取所属的a家连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.

根据以上信息解答下列问题:
(1)求a的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com