
【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=![]() (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣![]() t2+5t﹣
t2+5t﹣![]() )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣![]() t2+3t﹣
t2+3t﹣![]() )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣![]() x2+bx+c的顶点.
x2+bx+c的顶点.
①当点P在双曲线y=![]() 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=![]() 没有公共点;
没有公共点;
②当抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

【答案】(1)6,﹣6,(﹣![]() ,4);(2)①证明见解析;②t=
,4);(2)①证明见解析;②t=![]() 或t=
或t=![]() ;③
;③![]() .
.
【解析】(1)根据题意将相关数据代入.
(2)①用t表示直线MN解析式,及b,c,得到P点坐标带入双曲线y=![]() 解析式,证明关于t的方程无解即可;
解析式,证明关于t的方程无解即可;
②根据抛物线开口和对称轴,分别讨论抛物线过点B和在BD上时的情况;
③由②中部分结果,用t表示F、P点的纵坐标,求出t的取值范围及直线MN在四边形OAEB中所过的面积.
解:(1)∵A点坐标为(﹣6,0)
∴OA=6
∵过点C(﹣6,1)的双曲线y=![]()
∴k=﹣6
y=4时,x=![]()
∴点E的坐标为(﹣![]() ,4)
,4)
故答案为:6,﹣6,(﹣![]() ,4)
,4)
(2)①设直线MN解析式为:y1=k1x+b1
由题意得:
解得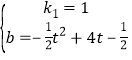 ,
,
∵抛物线y=﹣![]() 过点M、N,
过点M、N,
∴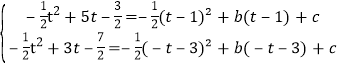 ,
,
解得![]()
∴抛物线解析式为:y=﹣![]() x2﹣x+5t﹣2
x2﹣x+5t﹣2
∴顶点P坐标为(﹣1,5t﹣![]() )
)
∵P在双曲线y=﹣![]() 上
上
∴(5t﹣![]() )×(﹣1)=﹣6
)×(﹣1)=﹣6
∴t=![]()
此时直线MN解析式为:
联立
∴8x2+35x+49=0
∵△=352﹣4×8×48=1225﹣1536<0
∴直线MN与双曲线y=﹣![]() 没有公共点.
没有公共点.
②当抛物线过点B,此时抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点
x2+bx+c与矩形OADB有且只有三个公共点
∴4=5t﹣2,得t=![]()
当抛物线在线段DB上,此时抛物线与矩形OADB有且只有三个公共点
∴![]() ,得t=
,得t=![]()
∴t=![]() 或t=
或t=![]()
③∵点P的坐标为(﹣1,5t﹣![]() )
)
∴yP=5t﹣![]()
当1≤t≤6时,yP随t的增大而增大
此时,点P在直线x=﹣1上向上运动
∵点F的坐标为(0,﹣![]() )
)
∴yF=﹣![]()
∴当1≤t≤4时,随者yF随t的增大而增大
此时,随着t的增大,点F在y轴上向上运动
∴1≤t≤4
当t=1时,直线MN:y=x+3与x轴交于点G(﹣3,0),与y轴交于点H(0,3)
当t=4﹣![]() 时,直线MN过点A.
时,直线MN过点A.
当1≤t≤4时,直线MN在四边形AEBO中扫过的面积为
S=![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某厂前5个月生产的总产量y(件)与时间x(月)的关系如图所示,则下列说法正确的是( )
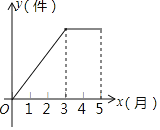
A. 1﹣3月的月产量逐月增加,4、5两月产量逐月减少
B. 1﹣3月的月产量逐月增加,4、5两月产量与3月持平
C. 1﹣3月的月产量逐月增加,4、5两月停产
D. 1﹣3月的月产量逐月持平,4、5两月停产
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类杜团的意愿,在全校随机抽取了50名学生进行问卷调查,问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如表:
社团名称 | A.酵素制作社团 | B.回收材料小制作社团 | C.垃圾分类社团 | D.环保义工社团 | E.绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
(1)填空:在统计表中,这5个数的中位数是 ;
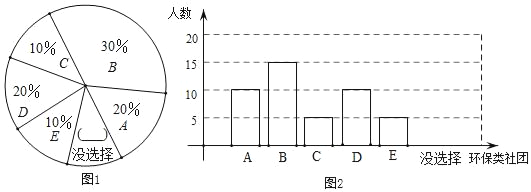
(2)根据以上信息,补全扇形图(图1)和条形图(图2);
(3)该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(4)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依次剪6张正方形纸片拼成如图示意的图形,图形中正方形①的面积为1,正方形②的面积为![]() .
.
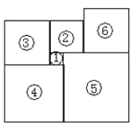
(1)请用含![]() 的式子直接写出正方形⑤的面积;
的式子直接写出正方形⑤的面积;
(2)若正方形⑥与正方形③的面积相等,求正方形④和正方形⑤的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,AB为⊙O的直径,过点A作⊙O的切线m;
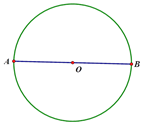
(2)在直线m上任取一点P(A点除外),连接PB交圆O与点C,请补全图形,并证明: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
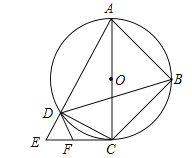
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=![]() ∶DE=4∶1,求DE的长.
∶DE=4∶1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
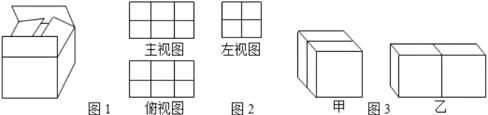
【题目】双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动,根据积木数量的不同,厂家会订制不同型号的外包装盒,所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1),长方体纸箱的长为![]() 厘米,宽为
厘米,宽为![]() 厘米,高为
厘米,高为![]() 厘米.
厘米.
(1)请用含有![]() ,
,![]() ,
,![]() 的代数式表示制作长方体纸箱需要________平方厘米纸板;
的代数式表示制作长方体纸箱需要________平方厘米纸板;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为多少个;
(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
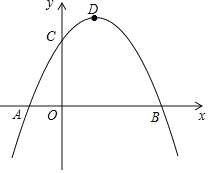
【题目】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;
(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com