练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某厂前5个月生产的总产量y（件）与时间x（月）的关系如图所示，则下列说法正确的是（　　）

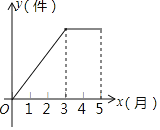
    A. 1﹣3月的月产量逐月增加，4、5两月产量逐月减少

    B. 1﹣3月的月产量逐月增加，4、5两月产量与3月持平

    C. 1﹣3月的月产量逐月增加，4、5两月停产

    D. 1﹣3月的月产量逐月持平，4、5两月停产

    【答案】D

    【解析】

    本题是一个分段函数，在1、2、3月该产品的总产量y（件）与时间x（月）的函数图象是正比例函数图象，4、5月总产量没有变化．

    解：根据图象得：

    1月至3月，该产品的总产量y（件）与时间x（月）的函数图象是正比例函数图象，

    所以每月产量是一样的，

    4月至5月，产品的总产量y（件）没有变化，即4月、5月停止了生产．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，O是AC上一动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F.若点O运动到AC的中点，则∠ACB=_____°时，四边形AECF是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】杨老师为了了解所教班级学生课后复习的具体情况，对本班部分学生进行了一个月的跟踪调查，然后将调查结果分成四类：A：优秀；B：良好；C：一般；D：较差．并将调查结果绘制成以下两幅不完整的统计图．

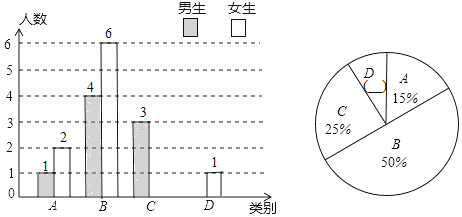
    请根据统计图解答下列问题：

    （1）本次调查中，杨老师一共调查了　 　名学生，其中C类女生有　 　名，D类男生有　 　名；

    （2）补全上面的条形统计图和扇形统计图；

    （3）在此次调查中，小平属于D类．为了进步，她请杨老师从被调查的A类学生中随机选取一位同学，和她进行“一帮一”的课后互助学习．请求出所选的同学恰好是一位女同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电子超市销售甲、乙两种型号的蓝牙音箱，每台进价分别为240元，140元，下表是近两周的销售情况：（销售收入=销售单价×销售数量）

    销售时段

    销售数量

    销售收入

    甲种型号

    乙种型号

    第一周

    3台

    7台

    2160元

    第二周

    5台

    14台

    4020元

    求甲、乙两种型号蓝牙音箱的销售单价．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用对称性可设计出美丽的图案．在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上)．

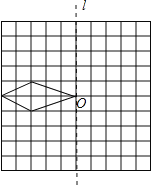
    (1)先作出该四边形关于直线成轴对称的图形，再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形；

    (2)完成上述设计后，整个图案的面积等于_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们定义：在一个三角形中，如果一个角的度数是另一个角度数的3倍，那么这样的三角形我们称之为“和谐三角形”．如：三个内角分别为105°，40°，35°的三角形是“和谐三角形”

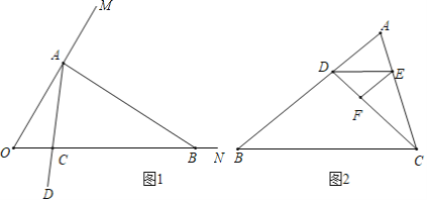
    概念理解：如图1，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O，B重合）

    （1）∠ABO的度数为______，△AOB______（填“是”或“不是”）“和谐三角形”；

    （2）若∠ACB=80°，求证：△AOC是“和谐三角形”．

    应用拓展：（3）如图2，点D在△ABC的边AB上，连接DC，作∠ADC的平分线交AC于点E，在DC上取点F，使∠EFC+∠BDC=180°，∠DEF=∠B．若△BCD是“和谐三角形”，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）解方程：4（x+1）2-169=0；

    （2）一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年是我市全面推进中小学校“社会主义核心价值观”教育年.某校对全校学生进行了中期检测评价,检测结果分为(优秀)、（良好）、（合格）、（不合格）四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表（图1）和统计图（图2）.

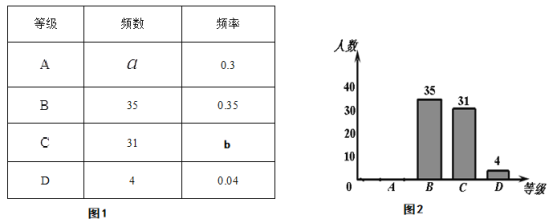
    请根据图1、图2提供的信息，解答下列问题：

    （1）本次随机抽取的样本容量为

    （2） , .

    （3）请在图2中补全条形统计图.

    （4）若该校共有学生800人，据此估算，该校学生在本次检测中达到“(优秀)”等级的学生人数为 人.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OADB的顶点A，B的坐标分别为A（﹣6，0），B（0，4）．过点C（﹣6，1）的双曲线y=（k≠0）与矩形OADB的边BD交于点E．

    （1）填空：OA=　 ，k=　 　，点E的坐标为　 　；

    （2）当1≤t≤6时，经过点M（t﹣1，﹣t2+5t﹣）与点N（﹣t﹣3，﹣t2+3t﹣）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣x2+bx+c的顶点．

    ①当点P在双曲线y=上时，求证：直线MN与双曲线y=没有公共点；

    ②当抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点，求t的值；

    ③当点F和点P随着t的变化同时向上运动时，求t的取值范围，并求在运动过程中直线MN在四边形OAEB中扫过的面积．

    查看答案和解析>>

    同步练习册答案