
【题目】我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
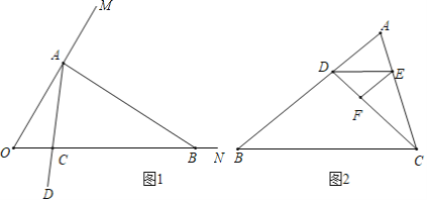
概念理解:如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为______,△AOB______(填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:(3)如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
【答案】(1)30,是;(2)证明见解析;(3)∠B=36°或∠B=![]()
【解析】
(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“和谐三角形”的概念判断;
(2)根据“和谐三角形”的概念证明即可;应用拓展:根据比较的性质得到∠EFC=∠ADC,根据平行线的性质得到∠DEF=∠ADE,推出DE∥BC,得到∠CDE=∠BCD,根据角平分线的定义得到∠ADE=∠CDE,求得∠B=∠BCD,根据“和谐三角形”的定义求解即可.
解:(1)∵AB⊥OM,
∴∠OAB=90°,
∴∠ABO=90°-∠MON=30°,
∵∠OAB=3∠ABO,
∴△AOB为“和谐三角形”,
故答案为:30;是;
(2)证明:∵∠MON=60°,∠ACB=80°,
∵∠ACB=∠OAC+∠MON,
∴∠OAC=80°-60°=20°,
∵∠AOB=60°=3×20°=3∠OAC,
∴△AOC是“和谐三角形”;
应用拓展:
∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴AD∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC,
∴∠CDE=∠BCD,
∵AE平分∠ADC,
∴∠ADE=∠CDE,
∴∠B=∠BCD,
∵△BCD是“和谐三角形”,
∴∠BDC=3∠B,或∠B=3∠BDC,
∵∠BDC+∠BCD+∠B=180°,
∴∠B=36°或∠B=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
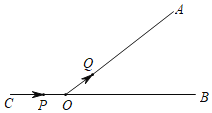
【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.
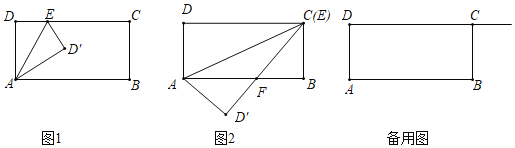
(1)当D′点落在AB边上时,∠DAE= °;
(2)如图2,当E点与C点重合时,D′C与AB交点F,
①求证:AF=FC;②求AF长.
(3)连接D′B,当∠AD′B=90°时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂前5个月生产的总产量y(件)与时间x(月)的关系如图所示,则下列说法正确的是( )
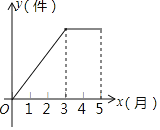
A. 1﹣3月的月产量逐月增加,4、5两月产量逐月减少
B. 1﹣3月的月产量逐月增加,4、5两月产量与3月持平
C. 1﹣3月的月产量逐月增加,4、5两月停产
D. 1﹣3月的月产量逐月持平,4、5两月停产
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=![]() (∠A+∠C).
(∠A+∠C).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD∥GE,AQ 平分∠FAC,交 BD 于 Q,∠GFA=50°,∠Q=25°,则∠ACB 的 度数( )
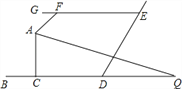
A. 90° B. 95° C. 100° D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]()
![]() 的图象过点
的图象过点![]() ,一次函数
,一次函数![]()
![]() 的图象
的图象![]() 经过点
经过点![]() .
.
(1)求![]() 值并写出二次函数表达式;
值并写出二次函数表达式;
(2)求![]() 值;
值;
(3)设直线![]() 与二次函数图象交于
与二次函数图象交于![]() 两点,过
两点,过![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,
试证明:![]() ;
;
(4)在(3)的条件下,请判断以线段![]() 为直径的圆与
为直径的圆与![]() 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,AB为⊙O的直径,过点A作⊙O的切线m;
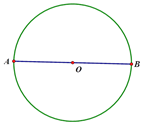
(2)在直线m上任取一点P(A点除外),连接PB交圆O与点C,请补全图形,并证明: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com