
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度![]() (cm)与所挂物体的质量
(cm)与所挂物体的质量![]() (kg)之间的关系如下表:
(kg)之间的关系如下表:
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
弹簧的长度 | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AC是□ABCD的一条对角线,过AC中点O的直线分别交AD、BC 于点E、F.

(1)求证:AE=CF;
(2)连接AF,CE.
①当EF⊥AC时,四边形AFCE是什么四边形?请证明你的结论;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
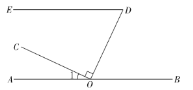
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.
(1)求证:DE是⊙O的切线;
(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:![]() 和完全平方公式:
和完全平方公式:![]() 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式![]()
![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()

![]()
![]() .
.
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将![]() 化成
化成![]() 的形式为_______;
的形式为_______;
(2)请你利用上述方法因式分解:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )

A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,![]() 、
、![]() 、
、![]() 均为格点(格点是指每个小正方形的顶点),将
均为格点(格点是指每个小正方形的顶点),将![]() 向下平移6个单位得到
向下平移6个单位得到![]() .利用网格点和直尺画图:
.利用网格点和直尺画图:

(1)在网格中画出![]() ;
;
(2)画出![]() 边上的中线
边上的中线![]() ,
,![]() 边上的高线
边上的高线![]() ;
;
(3)若![]() 的边
的边![]() 、
、![]() 分别与
分别与![]() 的边
的边![]() 、
、![]() 垂直,则
垂直,则![]() 的度数是 .
的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com