
【题目】如图,在正方形网格中,![]() 、
、![]() 、
、![]() 均为格点(格点是指每个小正方形的顶点),将
均为格点(格点是指每个小正方形的顶点),将![]() 向下平移6个单位得到
向下平移6个单位得到![]() .利用网格点和直尺画图:
.利用网格点和直尺画图:

(1)在网格中画出![]() ;
;
(2)画出![]() 边上的中线
边上的中线![]() ,
,![]() 边上的高线
边上的高线![]() ;
;
(3)若![]() 的边
的边![]() 、
、![]() 分别与
分别与![]() 的边
的边![]() 、
、![]() 垂直,则
垂直,则![]() 的度数是 .
的度数是 .
【答案】(1)见解析;(2)180°.
【解析】
(1)根据网格结构找出点A、B、C向下平移6个单位的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据四边形的内角和及垂直的定义解答即可;
(1)如图所示:直接把点平移,然后连接.
(2)如图所示:找AC的中点D,连接BD即可,延长AB过点C做垂线.

(3) 分两种情况解答:
①如图所示:

∵∠CAB=45°, ∠AFP=∠AEP=90°, ∴∠MPN=360°-∠AFP-∠AEP-∠CAB=360°-90°-90°-45°=135°;
②如图所示:

∵∠CAB=45°, ∠AFP=∠AEP=90°,,∠AOE=∠POF,,
∴360°-∠AFP-∠POF=360°-∠AEP -∠AOE, ∴∠MPN=∠CAB=45°,
综上所述:∠MPN的度数为:45°或135°.


科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
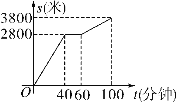
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列四种说法:①小明中途休息用了20分钟;②小明休息前爬山的平均速度为每分钟70米;③小明在上述过程中所走的路程为6600米;④小明休息前爬山的平均速度大于休息后爬山的平均速度.其中正确的是________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com