
【题目】如图,![]() 为
为![]() 的对角线的交点,过点
的对角线的交点,过点![]() 作直线
作直线![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
(3)若![]() ,直接写出
,直接写出![]() 的值为______.
的值为______.
【答案】(1)见解析;(2)12;(3)20.
【解析】
(1)由四边形ABCD是平行四边形,得到CD∥AB,OC=OA由平行线的性质得到∠OAB=∠OCD,推出△OAF≌△OCE(ASA).根据全等三角形的性质即可得到结论;
(2)根据△DEO≌△BFO得到OE=OF=1.5,BF=DE,于是得到EF=3,BF+CE=AB=5,即可得到结论;
(3)根据全等三角形的性质即可得到SABCD=2S四边形CEFB=10×2=20.
解:(1)证明:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() .
.![]() .
.
(2)同(1)可证△DEO≌△BFO(ASA).
∴OE=OF=1.5,BF=DE,
∴EF=3,BF+CE=AB=5,
∴四边形EFBC的周长=3+5+4=12
(3)∵△DEO≌△BFO,
∴S四边形CEFB=S△BCD,
∴SABCD=2S四边形CEFB=10×2=20,
故答案为20.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,![]() 、
、![]() 、
、![]() 均为格点(格点是指每个小正方形的顶点),将
均为格点(格点是指每个小正方形的顶点),将![]() 向下平移6个单位得到
向下平移6个单位得到![]() .利用网格点和直尺画图:
.利用网格点和直尺画图:

(1)在网格中画出![]() ;
;
(2)画出![]() 边上的中线
边上的中线![]() ,
,![]() 边上的高线
边上的高线![]() ;
;
(3)若![]() 的边
的边![]() 、
、![]() 分别与
分别与![]() 的边
的边![]() 、
、![]() 垂直,则
垂直,则![]() 的度数是 .
的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒2cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.(注:正方形的四边长都相等,四个角都是直角)
(1)CQ的长为______cm(用含![]() 的代数式表示);
的代数式表示);
(2)连接DQ并把DQ沿DC翻折,交BC延长线于点F.连接DP、DQ、PQ.
①若![]() ,求t的值.
,求t的值.
②当![]() 时,求t的值,并判断
时,求t的值,并判断![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
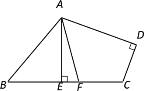
【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=-![]() 与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为![]() 的中点.
的中点.
(1)求证:OF∥BD;
(2)若点F为线段OC的中点,且⊙O的半径R=6 cm,求图中阴影部分(弓形)的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com