
【题目】如图,在边长为6cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒2cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.(注:正方形的四边长都相等,四个角都是直角)
(1)CQ的长为______cm(用含![]() 的代数式表示);
的代数式表示);
(2)连接DQ并把DQ沿DC翻折,交BC延长线于点F.连接DP、DQ、PQ.
①若![]() ,求t的值.
,求t的值.
②当![]() 时,求t的值,并判断
时,求t的值,并判断![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.

科目:初中数学 来源: 题型:
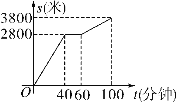
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列四种说法:①小明中途休息用了20分钟;②小明休息前爬山的平均速度为每分钟70米;③小明在上述过程中所走的路程为6600米;④小明休息前爬山的平均速度大于休息后爬山的平均速度.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,点F在AC延长线上,![]() ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的等边△ABC和△ADC,在平面上拼成菱形ABCD,把一个含60°角的三角尺与这个菱形重合,使三角尺有两边分别在AB、AC上,将三角尺绕点A按逆时针方向旋转.
(1)如图1,当三角尺的两边与BC、CD分别相交于点E、F时,观察或测量BE,CF的长度,你能得出什么结论?证明你的结论。

(2)如图2,当三角尺的两边与BC、CD的延长线分别交于E、F时,你在(1)中的结论还成立吗?请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com