
����Ŀ����ͼ�����κ���y=![]() x2+bx��
x2+bx��![]() ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��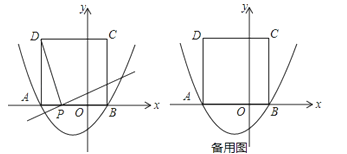
��1��b��ֵ����D�����ꡣ
��2���߶�AO���Ƿ���ڵ�P����P����A��O�غϣ���ʹ��OE�ij�Ϊ1��
��3����x�Ḻ�������Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
���𰸡��⣺��1���ߵ�A����3��0���ڶ��κ���y=![]() x2+bx��
x2+bx��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��0=![]() ��3b��
��3b��![]() �����b=1��
�����b=1��
����κ�������ʽΪy=![]() x2+x��
x2+x��![]() =
=![]() ��x+3����x��1����
��x+3����x��1����
���B��1��0����AB=1������3��=4��
���ı���ABCDΪ�����Σ�
��AD=AB=4��
���D����3��4����
�ʴ�Ϊ��1������3��4����
��2��ֱ��PE��y���ڵ�E����ͼ1��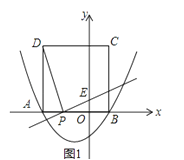
������ڵ�P��ʹ��OE�ij�Ϊ1����OP=a����AP=3��a��
��DP��AE����APD+��DPE+��EPO=180�㣬
���EPO=90�㩁��APD=��ADP��
tan��ADP=![]() =
=![]() ��tan��EPO=
��tan��EPO=![]() =
=![]() ��
��
��![]() =
=![]() ����a2��3a+4=0��
����a2��3a+4=0��
��=����3��2��4��4=��7����
���߶�AO�ϲ����ڵ�P����P����A��O�غϣ���ʹ��OE�ij�Ϊ1��
��3��������������ĵ�P��DE��x���ڵ�M����ͼ2��
�ߡ�PED�ǵ��������Σ�
��DP=PE��
��DP��PE���ı���ABCDΪ������
���EPO+��APD=90�㣬��DAP=90�㣬��PAD+��APD=90�㣬
���EPO=��PDA����PEO=��DPA��
�ڡ�PEO�͡�DAP�У�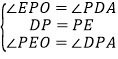 ��
��
���PEO�ա�DAP��
��PO=DA=4��OE=AP=PO��AO=4��3=1��
���P��������4��0����
��DA��x�ᣬ
��DA��EO��
���ADM=��OEM����ֱ��ƽ�У��ڴ�����ȣ���
�֡ߡ�AMD=��OME���Զ��ǣ���
���DAM��EOM��
��![]() =
=![]() =
=![]() ��
��
��OM+MA=OA=3��
��MA=![]() ��3=
��3=![]() ��
��
��PED��������ABCD�ص����֡�ADM���Ϊ![]() ��AD��AM=
��AD��AM=![]() ��4��
��4��![]() =
=![]() ��
��
�𣺴��������ĵ�P����P������Ϊ����4��1������ʱ��PED��������ABCD�ص����ֵ����Ϊ![]() ��
��
����������1�����õ��ڶ��κ���ͼ���ϣ����뼴�����b�������κ������ɽ���ʽ�����ܵó�B������꣬��AD=AB�����D�����ꣻ
��2��������ڣ���DP��AE���ҳ���EPO=��PDA�����õȽǵ�������ȣ��ɵó�һ������OP���ȵ�һԪ���η��̣��ɷ�����ɵ�֪�����������ĵ㣻
��3�����ýǺͱߵĹ�ϵ���ҵ�ȫ�ȣ����������������ƣ��������Ʊȼ������AM�������ADM�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0������˵����
��abc��0����2a��b=0����4a+2b+c��0����������5��y1������2��y2�����������ϵ����㣬��y1��y2 ��
����˵����ȷ���ǣ�������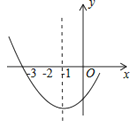
A.�٢�
B.�ڢ�
C.�ڢۢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
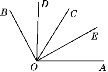
����Ŀ����ͼ��ODƽ�֡�BOC��OEƽ�֡�AOC����BOC��60�㣬��AOC��58��.
(1)�����AOB���䲹�ǵĶ�����
(2)���������DOC�͡�AOE�Ķ�����
���жϡ�DOE���AOB�Ƿ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
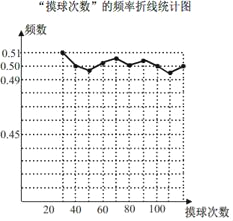
����Ŀ����һ������������װ����ɫ��ͬ�ĺڡ���������40����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣���ͼ����������������Ƶ������ͳ��ͼ��
��1������ͳ��ͼ�����������ڡ���������ɫ��������ٸ���
��2�����Ҫʹ��������ĸ���Ϊ![]() ����Ҫ���������ٷ�����ٸ�����
����Ҫ���������ٷ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD=CD����DAB=��ACB=90�㣬����D��DE��AC������ΪF��DE��AB�ཻ�ڵ�E��
��1����֤��ABAF=CBCD��
��2����֪AB=15cm��BC=9cm��P���߶�DE�ϵĶ��㣮��DP=x cm������BCDP�����Ϊycm2 ��
����y����x�ĺ�����ϵʽ��
��y�Ƿ�������ֵ���������������ֵ������������˵�����ɣ�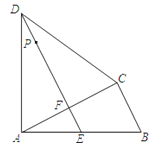
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
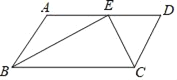
����Ŀ����֪����ͼ����ABCD�У�BE��CE�ֱ�ƽ����ABC����BCD��E��AD�ϣ�BE=12cm��CE=5cm����ABCD���ܳ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AC��BD�ǶԽ��ߣ�����DCB���ŵ�D˳ʱ����ת45���õ���DGH��HG��AB�ڵ�E������DE��AC�ڵ�F������FG�������н��ۣ�
���ı���AEGF�����Σ��ڡ�HED�������1��![]() ���ۡ�AFG=112.5�㣻��BC+FG=
���ۡ�AFG=112.5�㣻��BC+FG=![]() ��������ȷ�Ľ����ǣ�������
��������ȷ�Ľ����ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���y���x���ϣ���ABO��60�㣬������������һ��P��ʹ�á�PAB�ǵ��������Σ�����������ĵ�P���У� ��
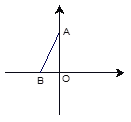
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���ACB=90�㣬AC=BC=4��DΪBC���е㣬
�У���ACB=90�㣬AC=BC=4��DΪBC���е㣬 ![]() ������ΪE.����B��BF//AC��DE���ӳ����ڵ�F������CF��AF.�������½��ۣ�
������ΪE.����B��BF//AC��DE���ӳ����ڵ�F������CF��AF.�������½��ۣ�
��BF=2����![]() ����ADƽ�֡�CAB����AF=
����ADƽ�֡�CAB����AF=![]() ������CAF=��CFB��������ȷ�Ľ�������������
������CAF=��CFB��������ȷ�Ľ�������������
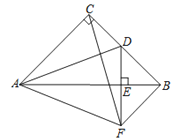
A. �٢ڢ� B. �٢ڢ� C. �ڢۢܢ� D. �٢ڢܢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com