
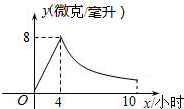
 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).分析 (1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)利用y=4分别得出x的值,进而得出答案.
解答 解:(1)当0≤x≤4时,设直线解析式为:y=kx,
将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设反比例函数解析式为:y=$\frac{a}{x}$,
将(4,8)代入得:8=$\frac{a}{4}$,
解得:a=32,
故反比例函数解析式为:y=$\frac{32}{x}$;
因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4),
下降阶段的函数关系式为y=$\frac{32}{x}$(4≤x≤10).
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=$\frac{32}{x}$,解得:x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
点评 此题主要考查了反比例函数的应用,根据题意得出函数解析式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a3+a2=2a5 | B. | (2ab2)3=6a3b6 | ||
| C. | 2a2b•3ab2=6a2b3 | D. | x3y2÷(-2x2y)=-$\frac{1}{2}$xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | +415m | B. | -415m | C. | ±415m | D. | -8848m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com