Question

△ABC中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，求∠A的度数．

Answer 1

解：∵4∠C=7∠A，
∴∠C=∠A，
∵∠A+∠B+∠C=∠A+∠B+∠A=180°，
∴∠B=180°-∠A，
∵∠A＜∠B＜∠C，
∴，
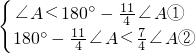
由①得，∠A＜48°，
由②得，∠A＞40°，
∴40°＜∠A＜48°，
∵∠A是整数，
∴∠A是4的整数倍，
∴∠A=44°．
分析：先用∠A表示出∠C，再根据三角形的内角和等于180°列式整理用∠A表示出∠B，再根据不等式求出∠A的取值范围，最后根据∠A是整数解答．
点评：本题考查了三角形的内角和定理，一元一次不等式组的解法，求出∠A的取值范围是解题的关键．