
为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
【考点】二次函数的应用.
【分析】(1)根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据利润=1盒粽子所获得的利润×销售量列式整理,再根据二次函数的最值问题解答;
(3)先由(2)中所求得的P与x的函数关系式,根据这种粽子的每盒售价不得高于58元,且每天销售粽子的利润不低于6000元,求出x的取值范围,再根据(1)中所求得的销售量y(盒)与每盒售价x(元)之间的函数关系式即可求解.
【解答】解:(1)由题意得,y=700﹣20(x﹣45)=﹣20x+1600;
(2)P=(x﹣40)(﹣20x+1600)=﹣20x2+2400x﹣64000=﹣20(x﹣60)2+8000,
∵x≥45,a=﹣20<0,
∴当x=60时,P最大值=8000元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得﹣20(x﹣60)2+8000=6000,
解得x1=50,x2=70.
∵抛物线P=﹣20(x﹣60)2+8000的开口向下,
∴当50≤x≤70时,每天销售粽子的利润不低于6000元的利润.
又∵x≤58,
∴50≤x≤58.
∵在y=﹣20x+1600中,k=﹣20<0,
∴y随x的增大而减小,
∴当x=58时,y最小值=﹣20×58+1600=440,
即超市每天至少销售粽子440盒.
【点评】本题考查的是二次函数与一次函数在实际生活中的应用,主要利用了利润=1盒粽子所获得的利润×销售量,求函数的最值时,注意自变量的取值范围.


科目:初中数学 来源: 题型:
由二次函数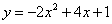 的图象如何平移就得到
的图象如何平移就得到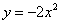 的图像( )
的图像( )
A.向左平移1个单位,再向上平移3个单位B.向右平移1个单位,再向上平移3个单位.
C.向左平移1个单位,再向下平移3个单位 D.向右平移1个单位,再向下平移3个单位。
查看答案和解析>>
科目:初中数学 来源: 题型:
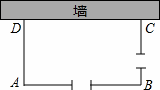
如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD)。
(1)若所用铁栅栏的长为40米,用含x的代数式表示矩形的长AB;
(2)在( 1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?
1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com