
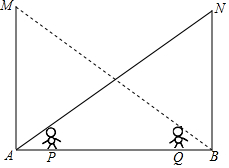
 如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.
如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽. 分析 根据题意结合图形可知,图中AP=BQ,在点P处时,△APC和△ABN相似,然后利用相似三角形对应边成比例列出比例式,再利用AP=$\frac{1}{2}$(AB-PQ),然后整理求解即可.
解答 解:如图,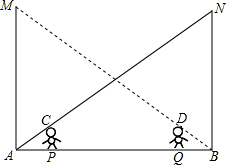
由题意知:
PQ=6米,AM=BN=9.6米,CP=DQ=1.6米,AP=QB,
在△APC和△ABN中,
∵∠CAP=∠NAB,∠APC=∠ABN=90°,
∴△AMP∽△ADB,
∴$\frac{AP}{AB}=\frac{CP}{BN}$,
即$\frac{\frac{1}{2}(AB-6)}{AB}=\frac{1.6}{9.6}$,
解得AB=9.
答:两个路灯之间的距离是9米.
点评 本题主要考查了相似三角形的应用,熟练掌握相似三角形对应边成比例的性质是解题的关键,本题看出AP=BQ对解题非常重要.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知数轴上有A,B,C三个点,如图所示,它们表示的数分别是-18,-6,14.
已知数轴上有A,B,C三个点,如图所示,它们表示的数分别是-18,-6,14.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2,-1,0,1,2,3 | B. | -2,-1,0,1,2 | C. | -2,-1,0,1,2,3 | D. | -1,0,1,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工程总量 | 所用时间(天) | 工程效率 | |
| 甲队 | 1 | x | $\frac{1}{x}$ |
| 乙队 | 1 | x+6 | $\frac{1}{x+6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
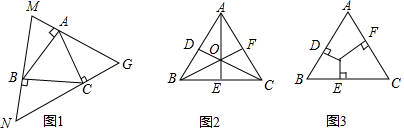
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
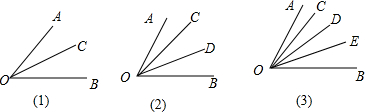
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com