
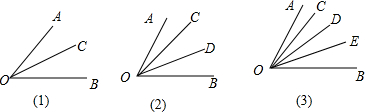
分析 有公共顶点的n条射线,可构成$\frac{1}{2}$n(n-1)个角,依据规律回答即可.
解答 解:∠AOB的顶点引1条射线,图中共有3个角;
∠AOB的顶点引2条射线,$\frac{4×3}{2}$=6,故共有6个角;
∠AOB的顶点引3条射线,$\frac{5×4}{2}$=10,故共有10个角;
∠AOB的顶点引n条射线,$\frac{(n+1)(n+2)}{2}$,故共有$\frac{(n+1)(n+2)}{2}$个角.
故答案为:3;6;10;$\frac{(n+1)(n+2)}{2}$.
点评 本题主要考查的是角的概念,掌握其规律是解题的关键.有公共顶点的n条射线,一共可构成$\frac{1}{2}$n(n-1)个角.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
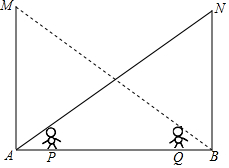 如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.
如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
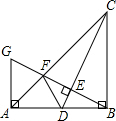 如图,在Rt△ABC中,∠ABC=90°,BA=BC=4,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于CD的直线相交于点G,连接DF,求四边形ADEF的周长.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=4,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于CD的直线相交于点G,连接DF,求四边形ADEF的周长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠ACB=90°,分别以边AB、AC、BC为边分别向外作等边三角形,其面积分别为S1,S2,S3,若S1=6,S2=2,则S3=8.
如图,Rt△ABC中,∠ACB=90°,分别以边AB、AC、BC为边分别向外作等边三角形,其面积分别为S1,S2,S3,若S1=6,S2=2,则S3=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com