
【题目】已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3).
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
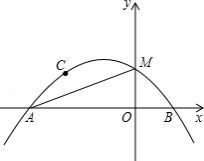
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚硬币,正面一定朝上
B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C.旅客上飞机前的安检应采用抽样调查
D.方差越大,数据的波动越大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答:
(1)△BDE是
(2)BC的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( ) 
A.180°
B.360°
C.540°
D.720°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在弧AQ上且不与A点重合,但Q点可与B点重合.
(1)弧AP的长与弧QB的长之和为定值l,请直接写出l的值;
(2)请直接写出点M与AB的最大距离,此时点P,A间的距离;点M与AB的最小距离,此时半圆M的弧与AB所围成的封闭图形面积.
(3)当半圆M与AB相切时,求弧AP的长.
(注:结果保留π,cos 35°=![]() ,cos 55°=
,cos 55°=![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com