

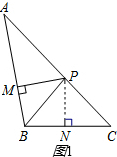
 (1)解:如图1所示.(1分)
(1)解:如图1所示.(1分)| 1 |
| 2 |
| 1 |
| 2 |
| S△ABP |
| S△BPC |
| AB |
| BC |
| 30 |
| 23 |
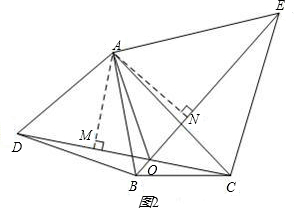 ∴AD=AB,AC=AE,∠DAB=∠CAE=60°.
∴AD=AB,AC=AE,∠DAB=∠CAE=60°.| 1 |
| 2 |
| 1 |
| 2 |
|


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011—2012学年北京市首师大附中八年级上学期期中考试数学试卷(带解析) 题型:解答题
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM AB于M,PN
AB于M,PN BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
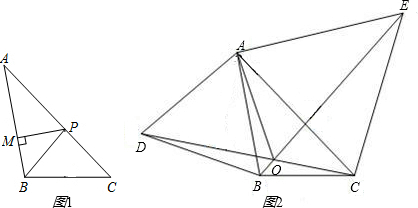
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断 AOD与
AOD与 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出 B和
B和 D的数量关系.
D的数量关系.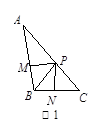
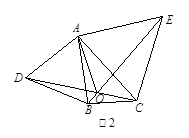
查看答案和解析>>
科目:初中数学 来源:2013届北京市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM AB于M,PN
AB于M,PN BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断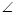 AOD与
AOD与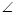 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分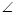 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出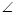 B和
B和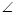 D的数量关系.
D的数量关系.
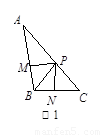
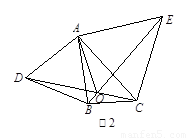
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com