
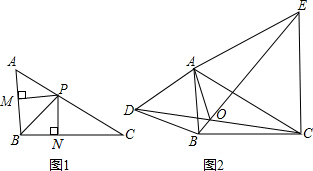
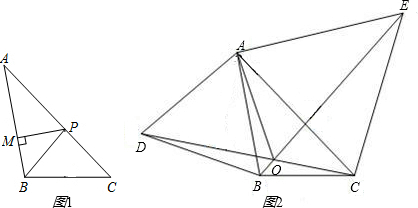
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM AB于M,PN
AB于M,PN BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断 AOD与
AOD与 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出 B和
B和 D的数量关系.
D的数量关系.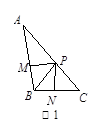
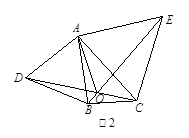
(1)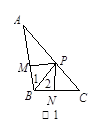
∵ 平分
平分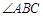
∴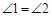
在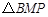 和
和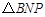 中
中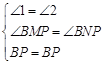
∴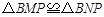
∴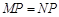
∵
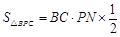
∴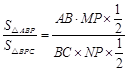
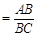
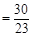
∴所求面积比值为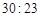
(2)答:∠AOD与∠AOE的数量关系为相等.
证明:如图2,过点A作AM⊥DC于M,AN⊥BE于N,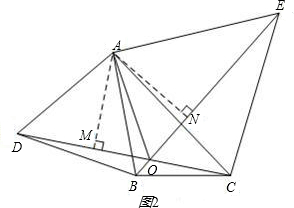
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°.
∵∠BAC=∠CAB,
∴∠DAC=∠BAE.
∴△DAC≌△BAE.
∴DC=BE,
∴S△DAC=S△BAE.
∵S△DAC=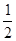 DC•AM,S△BAE=
DC•AM,S△BAE=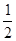 BE•AN,
BE•AN,
∴AM=AN.
∴点A在∠DOE的角平分线上.
∴∠AOD=∠AOE.
(3)作CM⊥AB,CN⊥AD,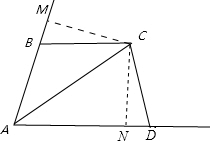
∵AC为∠BAD的角平分线,
∴CM=CN,
∵CB=DC,
∴△CMB≌△CND,
∴∠MBC=∠NDC,
∵∠MBC+∠ABC=180°,
∴∠ADC+∠ABC=180°,即∠B+∠D=180°.
解析


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届北京市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM AB于M,PN
AB于M,PN BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断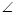 AOD与
AOD与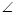 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出 B和
B和 D的数量关系.
D的数量关系.
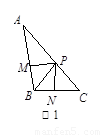
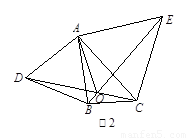
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com