
ij�̳�����ij��Ʒ�Ƶ��ֻ�,ÿ��������Ϊ2500Ԫ.�г����б����������ۼ�Ϊ2900Ԫʱ,ƽ��ÿ�����۳�8�����������ۼ�ÿ����50Ԫʱ,ƽ��ÿ����ܶ��۳�4��.
��1�����ۼ�Ϊ2800Ԫʱ,�����ֻ�ƽ��ÿ�����������ﵽ����Ԫ?
��2������ÿ���ֻ�����xԪ,ÿ�����������ΪyԪ,��д��y��x֮��ĺ�����ϵʽ��
��3���̳�Ҫ�����������,ÿ���ֻ����ۼ�Ӧ��Ϊ����Ԫ����ʱ����������Ƕ���Ԫ��
��1�����ۼ�Ϊ2800Ԫʱ,�����ֻ�ƽ��ÿ�����������ﵽ4800Ԫ��
��2�� ��
��
��3��ÿ̨�ʵ罵��150Ԫʱ,�̳�ÿ���������ֲʵ���������,���������5000Ԫ��
��������
�����������1�����ۼ�Ϊ2800Ԫʱ,���ۼ۽���100Ԫ,ƽ��ÿ������۳�16��.�������ÿ������
��2�����ݣ�����=��ÿ̨ʵ���ۼ۩�ÿ̨���ۣ���������,ÿ̨ʵ���ۼ�=2900��x,������=8+4��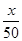 ,�к�����ϵʽ��
,�к�����ϵʽ��
��3�����ö��κ����Ķ������깫ʽ,���������ֵ��
�����������1�����ۼ�Ϊ2800Ԫʱ,���ۼ۽���100Ԫ,ƽ��ÿ������۳�16��.
���ԣ������ֻ�ƽ��ÿ�����������Ϊ��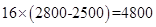 ��Ԫ����
��Ԫ����
��2����������,��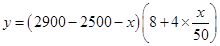 ,
,
�� ��
��
��3������ ,
,
��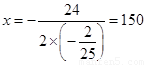 ʱ,
ʱ,
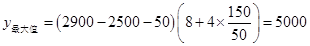
����,ÿ̨�ʵ罵��150Ԫʱ,�̳�ÿ���������ֲʵ���������,���������5000Ԫ��
���㣺���κ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 24��ij�̳�����ij��Ʒ�ƵĴ�ţ�̣���֪����Ϊÿ��40Ԫ����������Ҫ��ÿ���ۼ���40Ԫ��70Ԫ֮�䣮�г����鷢�֣���ÿ����50Ԫ���ۣ�ƽ��ÿ�������90�䣬�۸�ÿ����1Ԫ��ƽ��ÿ�������3�䣬�۸�ÿ����lԪ��ƽ��ÿ��������3�䣮
24��ij�̳�����ij��Ʒ�ƵĴ�ţ�̣���֪����Ϊÿ��40Ԫ����������Ҫ��ÿ���ۼ���40Ԫ��70Ԫ֮�䣮�г����鷢�֣���ÿ����50Ԫ���ۣ�ƽ��ÿ�������90�䣬�۸�ÿ����1Ԫ��ƽ��ÿ�������3�䣬�۸�ÿ����lԪ��ƽ��ÿ��������3�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com