练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图，点P是平面坐标系中一点，则点P到原点的距离是（　　）
    A、3
    B、
    		2
    C、
    		7
    D、
    		53
    分析：连接PO，在直角坐标系中，根据点P的坐标是（
    		2
    ，
    		7
    ），可知P的横坐标为
    		2
    ，纵坐标为
    		7
    ，然后利用勾股定理即可求解．
    解答：精英家教网解：连接PO，∵点P的坐标是（
    		2
    ，
    		7
    ），
    ∴点P到原点的距离=
    		2
    2    + 
    		7
    2
    =3．
    故选A．
    点评：此题主要考查学生对勾股定理、坐标与图形性质的理解和掌握，解答此题的关键是明确点P的横坐标为
    		2
    ，纵坐标为
    		7
    ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

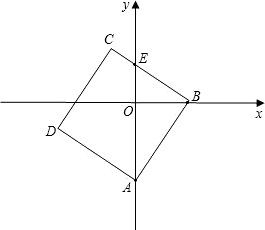    已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形A精英家教网BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
    （1）当t=3时，求点C的坐标；
    （2）当t＞0时，求m与t之间的函数关系式；
    （3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：江苏省如东县2012年中考网上阅卷适应性训练数学试题 题型：044

    如图，抛物线y＝ax2－2ax－3a(a＜0)，与x轴的交于A、B两点(点A在点B的右侧)，与y轴的正半轴交于点C，顶点为D

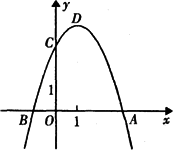
    (1)求顶点D的坐标(用含a的代数式表示)；

    (2)若以AD为直径的圆经过点C、①求抛物线的解析式；

    ②如图，点E是y轴负半轴上的一点，连结BE，将△OBE绕平面内某一点旋转180°，得到△PMN(点P、M、N分别和点O、B、E对应)，并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF＝1：2，求点M、N的坐标；

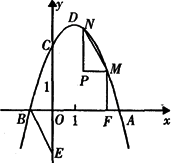
    ③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图，求点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

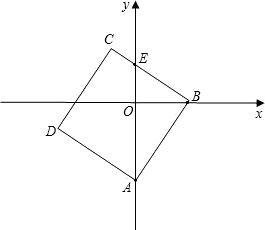    已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形A作业宝BCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
    （1）当t=3时，求点C的坐标；
    （2）当t＞0时，求m与t之间的函数关系式；
    （3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012年江苏省徐州市睢宁县新世纪中学中考数学模拟试卷（解析版） 题型：解答题

    已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
    （1）当t=3时，求点C的坐标；
    （2）当t＞0时，求m与t之间的函数关系式；
    （3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2010年浙江省金衢十一校联考中考数学模拟试卷（解析版） 题型：解答题

    （2013•惠山区一模）已知：如图，点O是平面直角坐标系的原点，点A的坐标为（0，-4），点B为x轴上一动点，以线段AB为边作正方形ABCD（按逆时针方向标记），正方形ABCD随着点B的运动而随之相应变动．点E为y轴的正半轴与正方形ABCD某一边的交点，设点B的坐标为（t，0），线段OE的长度为m．
    （1）当t=3时，求点C的坐标；
    （2）当t＞0时，求m与t之间的函数关系式；
    （3）是否存在t，使点M（-2，2）落在正方形ABCD的边上？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案