

分析 (1)如图1中,过C作CD⊥AB.线段CD即为△ABC的“等分积周线”.根据直角三角形斜边中线的性质即可求出CD的长.
(2)不能.当E为AB中点时,S△BCE=S△ACE,由BE=AE,AC≠BC,可知C△BCE≠C△ACE,所以CE不可能是△ABC的“等分积周线”.
(3)如图3中,过D作DE⊥BC,则AB=DE=4,首先求出四边形ABCD的面积、周长,分三种情形讨论即可解决问题.
解答 解:(1)如图1中,过C作CD⊥AB.线段CD即为△ABC的“等分积周线”.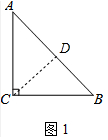
∵∠ACB=90°,∠ABC=45°
∴∠A=∠B=45°,
∴CA=CB,∵CD⊥AB,
∴AD=DB,
∴CD=$\frac{1}{2}$AB=2;
(2)不能.
理由:如图2中,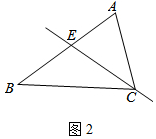
当E为AB中点时,S△BCE=S△ACE,
∵BE=AE,AC≠BC,
∴C△BCE≠C△ACE
∴所以CE不可能是△ABC的“等分积周线”.
(3)如图3中,过D作DE⊥BC,则AB=DE=4,
∵CD=5,
∴CE=3,
∵BC=6,
∴BE=AD=3,
∴S四边形ABCD=18,C四边形ABCD=18.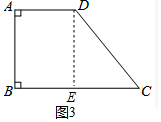
①如图4中,当直线l交AD、BC于M、N.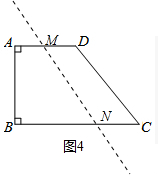
设BN=x,则AM=9-4-x=5-x,
S四边形ABNM=$\frac{1}{2}$(5-x+x)•4=10≠9,不成立
②如图5中,当直线l交AB、BC于M、N.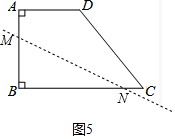
设BN=x,BM=9-x,
则S△BMM=$\frac{1}{2}$•x(9-x)=9,
解得x=6或3(舍弃,此时BM>4),
∴BF=6.
③如图6中,当直线l交CD、BC于M、N.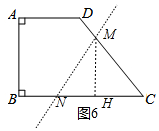
设CN=x,CM=9-x,作MH⊥BC于H,易知MH=$\frac{4}{5}$(9-x),
∴S△CMN=$\frac{1}{2}$•x•$\frac{4}{5}$(9-x)=9,
∴2x2-18x+45=0,
△=-36<0,此种情形不存在.
综上所述,水渠的位置如图7所示,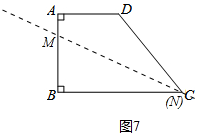
此时水渠与BC边的交点到点B的距离是6.
点评 本题考查三角形的面积、周长、直角梯形的性质、等腰直角三角形的性质、“等分积周线”的定义等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,学会分类讨论解决问题,属于中考压轴题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
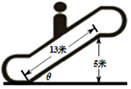 如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )
如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )| A. | $\frac{5}{13}$ | B. | $\frac{13}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com