练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是菱形，对角线AC与BD相交于O，AB=5，AO=4，求BD的长．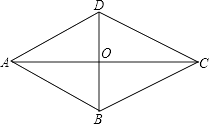

    【答案】解：∵四边形ABCD是菱形，对角线AC与BD相交于O，
    ∴AC⊥BD，DO=BO，
    ∵AB=5，AO=4，
    ∴BO= =3，
    ∴BD=2BO=2×3=6
    【解析】根据菱形的性质得出AC⊥BD，再利用勾股定理求出BO的长，即可得出答案．
    【考点精析】通过灵活运用勾股定理的概念和菱形的性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
    （1）求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
    （2）当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若正多边形的内角和是1080°，则该正多边形的边数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个三角形的两边长分别是4和8，若三角形是等腰三角形，那么周长是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个多边形，它的内角和比外角和的3倍多180°，求这个多边形的边数及内角和度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小红用一张长方形纸片ABCD进行折纸，已知AB=8cm，BC=10cm．当小红折叠时，顶点D落在BC边上的点F处（折痕为AE），求EC．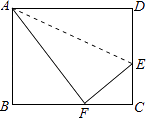

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在边长为1的小正方形组成的方格纸中，若多边形的每个顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形.记格点多边形内的格点数为，边界上的格点数为，则格点多边形的面积可表示为，其中， 为常数.

    （1）在下面的两张方格纸中各有一个格点多边形，依次为、正方形.认真数一数： 内的格点数是_______，正方形边界上的格点数是_______;

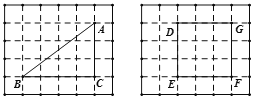
    （2）利用（1）中的两个格点多边形确定， 的值;

    （3）现有一张方格纸共有110个格点，画有一个格点多边形，它的面积，若该格点多边形外的格点数为.

    ①填空：若，则＝　　　　　；

    ②若，求的值．(写出解答过程)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．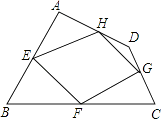

    （1）四边形EFGH的形状是 ， 并证明你的结论．
    （2）当四边形ABCD的对角线满足条件时，四边形EFGH是矩形；
    （3）你学过的哪种特殊四边形的中点四边形是矩形？
    （4）当四边形ABCD的对角线满足条件时，四边形EFGH是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD中，AB=4，对角线交于点O，F是BO的中点，连接AF，求AF的长度．

    查看答案和解析>>

    同步练习册答案