
��ͼ����֪���������� ��ͼ���ڶ������ڵĵ�A����1��m����AB��x���ڵ�B����AOB �����Ϊ2����ֱ�� y="ax+b" ������A�����Ҿ�������������
��ͼ���ڶ������ڵĵ�A����1��m����AB��x���ڵ�B����AOB �����Ϊ2����ֱ�� y="ax+b" ������A�����Ҿ������������� ��ͼ������һ��C��n��һ2����
��ͼ������һ��C��n��һ2����

��1���������� ��ֱ��y=ax+b�Ľ���ʽ��
��ֱ��y=ax+b�Ľ���ʽ��
��2����������������ֱ��д������ʽ ax+b�� �Ľ⼯_________________;
�Ľ⼯_________________;
��3������߶�OA�ij�����˼������x�����Ƿ����һ��P,ʹ�á�PAO�ǵ��������Σ�������ڣ������P�����꣬��������ڣ���˵�����ɡ�
��1��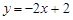
��2��x��-1 �� 0��x��2 ��3����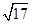 ��0������-
��0������-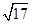 ��0������-2,0������-8.5��0��
��0������-2,0������-8.5��0��
��������
�����������1���ߵ�A��-1��m���ڵڶ������ڣ���AB = m��OB = 1����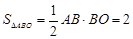
����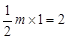 �����
����� ����A (-1,4)�� 1
��
����A (-1,4)�� 1
��
�ߵ�A (-1,4)���ڷ���������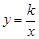 ��ͼ���ϣ���4 =
��ͼ���ϣ���4 =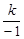 �����
����� ��
��
�෴��������Ϊ �� 2
��
�� 2
��
�֡߷��������� ��ͼ��C��n��
��ͼ��C��n��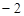 ����
����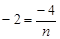 �����
�����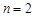 ����C (2,-2)��
����C (2,-2)��
��ֱ��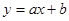 ����A (-1,4)��C
(2,-2)
����A (-1,4)��C
(2,-2)
��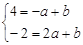 �ⷽ�����
�ⷽ����� 
��ֱ��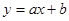 �Ľ���ʽΪ
�Ľ���ʽΪ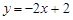 �� 4��
�� 4��
(2) x��-1 �� 0��x��2 6��
��3�����ڡ�P������Ϊ����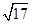 ��0������-
��0������-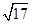 ��0������-2,0������-8.5��0��
��0������-2,0������-8.5��0��
��ÿ�����1�֣�
���㣺һ�κ���������������
�������������ڶ�һ�κ����ͷ����������Ļ���֪ʶ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| m |
| x |
| 4 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y1=
��ͼ����֪����������y1=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com