31、问题1：同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便，快捷．相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．
例：用简便方法计算195×205．
解：195×205
=（200-5）（200+5）①
=200
2-5
2②
=39975
（1）例题求解过程中，第②步变形是利用
平方差公式
（填乘法公式的名称）；
（2）用简便方法计算：9×11×101×10001．
问题2：对于形如x
2+2ax+a
2这样的二次三项式，可以用公式法将它分解成（x+a）
2的形式．但对于二次三项式x
2+2ax-3a
2，就不能直接运用公式了．此时，我们可以在二次三项式x
2+2ax-3a
2中先加上一项a
2，使它与x
2+2ax的和成为一个完全平方式，再减去a
2，整个式子的值不变，于是有：
x
2+2ax-3a
2=（x
2+2ax+a
2）-a
2-3a
2=（x+a）
2-（2a）
2=（x+3a）（x-a）．
像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．
（1）利用“配方法”分解因式：a
2-4a-12．
问题3：若x-y=5，xy=3，求：①x
2+y
2；②x
4+y
4的值．
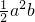和x2-y2+2x-1中，单项式是________，单项式的系数是________，次数是________，多项式是________，项是________，它是________次________项式，其中，二次项是________．
a2b -
