
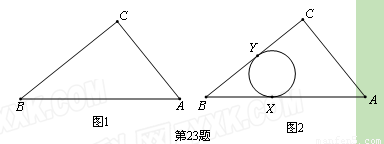
如图1,Rt△ABC两直角边的边长为AC=1,BC=2.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边CB相切于点Y.请你在图2中作出并标明⊙O的圆心O;(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为s,你认为能否确定s的最大值?若能,请你求出s的最大值;若不能,请你说明不能确定s的最大值的理由.
解:(1)共2分.(标出了圆心,没有作图痕迹的评1分)看见垂足为Y(X)的一 条 垂 线 (或 者∠ABC的平分线)即评1分,
(2)①当⊙P与Rt△ABC的边 AB和BC相切时,由角平分线的性质,动点P是∠ABC的平分线BM上的点.
如图1,在∠ABC的平分线BM上任意确定点P1 (不为∠ABC的顶点),
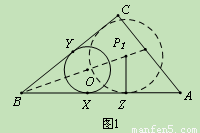
∵ OX =BOsin∠ABM, P1Z=BP1sin∠ABM.
当 BP1>BO 时 ,P1Z>OX,即P与B的距离越大,⊙P的面积越大.
这时,BM与AC的交点P是符合题意的、BP长度最大的点.
(3分.此处没有证明和结论不影响后续评分)
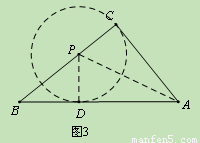
如图2,∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上.
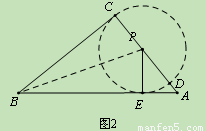
∴以P为圆心、PC为半径作圆,则⊙P与边CB相切于C,与边AB相切于E,
即这时的⊙P是符合题意的圆.(4分.此处没有证明和结论不影响后续评分)
这时⊙P的面积就是S的最大值.
∵∠A=∠A,∠BCA=∠AEP=90°,∴ Rt△ABC∽Rt△APE, (5分)
∴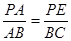 .
.
∵AC=1,BC=2,∴AB=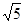 .
.
设PC=x,则PA=AC-PC=1-x, PC=PE,
∴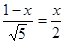 ,
∴x=
,
∴x=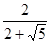 .
(6分)
.
(6分)
②如图3,同理可得:当⊙P与Rt△ABC的边AB和AC相切时,设PC=y,则 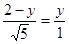 ,
,
∴y= 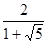 .
(7分)
.
(7分)
③如图4,同理可得:当⊙P与Rt△ABC的边BC和AC相切时,
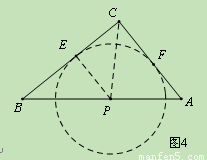
设PF=z,则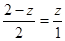 ,
∴z=
,
∴z=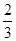 . (8分)
. (8分)
由①,②,③可知:∵ 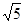 >2,∴
>2,∴ 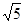 +2>
+2>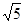 +1>3,
+1>3,
∵当分子、分母都为正数时,若分子相同,则分母越小,这个分数越大,
(或者:∵x= 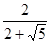 =2
=2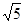 -4,
y=
-4,
y=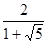 =
=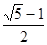 5,
5,
∴y-x=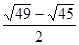 >0,
∴y>x. ∵z-y=
>0,
∴y>x. ∵z-y=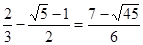 >0)
>0)
∴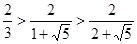 2, (9分,没有过程直接得出酌情扣1分)
2, (9分,没有过程直接得出酌情扣1分)
∴ z>y>x.
∴⊙P的面积S的最大值为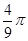 .
(10分)
.
(10分)
【解析】略


科目:初中数学 来源: 题型:
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
| ||
| 2 |
| AC |
| CM |
| BC |
| CA |
| CM |
| AB |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为2
| ||
| π |
2
| ||
| π |
查看答案和解析>>
科目:初中数学 来源: 题型:
 的外接圆.
的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com